シグモイド活性化関数のPythonによる実装
このチュートリアルでは、シグモイド活性化関数について学びます。シグモイド関数は常に0から1の間の出力を返します。
このチュートリアルの後、あなたは以下を理解するでしょう:
- What is an activation function?
- How to implement the sigmoid function in python?
- How to plot the sigmoid function in python?
- Where do we use the sigmoid function?
- What are the problems caused by the sigmoid activation function?
- Better alternatives to the sigmoid activation.
活性化関数とは何ですか?
活性化関数とは、ニューラルネットワークの出力を制御する数学的な関数です。活性化関数は、ニューロンが発火するかどうかを判断するのに役立ちます。
いくつかの人気のある活性化関数は次のとおりです。
- Binary Step
- Linear
- Sigmoid
- Tanh
- ReLU
- Leaky ReLU
- Softmax
活性化はニューラルネットワークモデルの出力に非線形性を追加する役割を担っています。活性化関数がないと、ニューラルネットワークは単純な線形回帰になります。
ニューラルネットワークの出力を計算するための数学式は次の通りです:
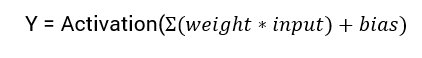
このチュートリアルでは、シグモイド活性化関数に焦点を当てます。この関数は数学のシグモイド関数から派生しています。
関数の公式について話し合いを始めましょう。
シグモイド活性化関数の公式
数学的には、シグモイド活性化関数は以下のように表すことができます。
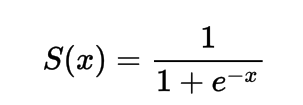
分母が常に1より大きいことが分かりますので、出力は常に0から1の間になることがわかります。
Pythonでシグモイド活性化関数の実装を行う。
このセクションでは、Pythonでシグモイド活性化関数を実装する方法を学びます。
Pythonで関数を定義することができます。
import numpy as np
def sig(x):
return 1/(1 + np.exp(-x))
いくつかの入力で関数を実行してみましょう。
import numpy as np
def sig(x):
return 1/(1 + np.exp(-x))
x = 1.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))
x = -10.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))
x = 0.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))
x = 15.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))
x = -2.0
print('Applying Sigmoid Activation on (%.1f) gives %.1f' % (x, sig(x)))
出力:
Applying Sigmoid Activation on (1.0) gives 0.7
Applying Sigmoid Activation on (-10.0) gives 0.0
Applying Sigmoid Activation on (0.0) gives 0.5
Applying Sigmoid Activation on (15.0) gives 1.0
Applying Sigmoid Activation on (-2.0) gives 0.1
Pythonを使用してSigmoid Activationをプロットする
シグモイド活性化関数をプロットするために、Numpyライブラリを使用します。
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 50)
p = sig(x)
plt.xlabel("x")
plt.ylabel("Sigmoid(x)")
plt.plot(x, p)
plt.show()
出力:
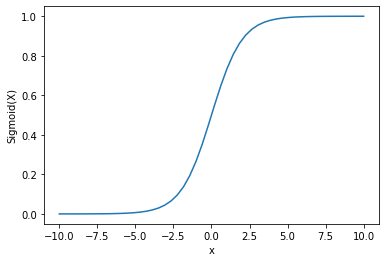
出力が0から1の間にあることがわかります。
確率は常に0から1の間にあるため、シグモイド関数はよく確率の予測に使用されます。
シグモイド関数の欠点の1つは、終端領域ではY値がX値の変化に対して非常に反応しづらいことです。
これにより、消失勾配問題として知られる問題が生じます。
勾配の消失は学習プロセスを遅くし、したがって望ましくないです。
この問題を克服するための代替案について話し合いましょう。 (Kono mondai o kokufuku suru tame no daitan’an ni tsuite hanashi aimashou.)
ReLu(Rectified Linear Unit)活性化関数。
勾配消失の問題を解決するより良い代替手段は、ReLu活性化関数です。
ReLu(ランプ)活性化関数は、入力が負の場合は0を返し、それ以外の場合は入力値をそのまま返す。
数学的に表されると、以下のようになります。
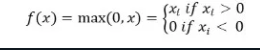
Pythonで以下のように実装できます。
def relu(x):
return max(0.0, x)
いくつかの入力に対して、どのように動作するか見てみましょう。
def relu(x):
return max(0.0, x)
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
出力:
Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0
ReLuに問題があるのは、負の入力に対する勾配がゼロになってしまうことです。
これは再び、負の入力に対して消失勾配(ゼロ勾配)の問題に繋がります。
この問題を解決するために、私たちには別の選択肢があります。それはリークReLU活性化関数として知られています。
リーキーReLU活性化関数
リークReLUは、負の値に対して非常に小さな線形成分のxを与えることで、ゼロ勾配の問題に対処しています。
数学的には、それを次のように定義することができます。 (Sūgakuteki ni wa, sore o tsugi no yō ni teigi suru koto ga dekimasu.)
f(x)= 0.01x, x<0
= x, x>=0
Pythonを使用して実装することができます。
def leaky_relu(x):
if x>0 :
return x
else :
return 0.01*x
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
出力:
Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2
結論
このチュートリアルはシグモイド活性化関数についてでした。私たちは、その関数をPythonで実装してプロットする方法を学びました。

