バイナリツリーにおけるレベルオーダートラバーサル
レベルオーダートラバーサルは、バイナリツリーを横断するための手法の一つです。この記事では、このアルゴリズムをC/C++で実装する方法について見ていきます。
しかし、その前に、私たちの概念をしっかり考えてみましょう。
概念の構築
バイナリツリーは、各ノードが最大で2つの子を持つデータ構造です。一番上のノードはルートノードと呼ばれます。
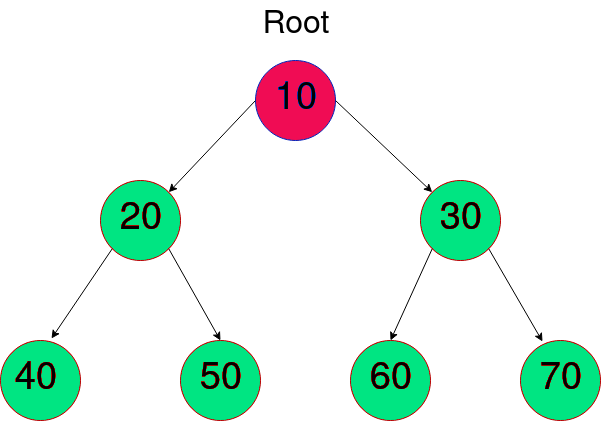
Binary Treeのノードを走査する一般的な方法は、次の4つあります。
- In order Traversal
- Pre Order Traversal
- Post Order Traversal
- Level Order Traversal
バイナリツリーのレベルとは何かを理解しましょう。
与えられたツリーのノードに対応する親ノードの数をレベルといいます。基本的には、そのノードからルートノードまでの祖先の数です。
したがって、根ノード(最上位ノード)のレベルは0です。なぜなら、そのノードには親が存在しないからです。もし子ノードがある場合、それらのどちらもレベル1になります。なぜなら、ルートノードまでの先祖はただひとつであり、それがルートノード自体だからです。
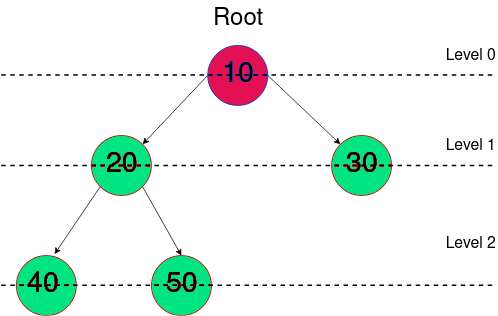
私たちはまた、二分木における高さの概念を理解する必要もあります。これは単純に、木の根から最も深いノードまでのパスの長さです。
この場合、木の高さは最も深いノード(40または50)からルートまでの長さとなります。したがって、木の高さは2です。
私達が概念を理解したので、レベル順トラバーサルの実装方法について理解しましょう。
レベルオーダートラバーサル
レベル順トラバーサルは、常に木のレベルに基づいてトラバースするトラバーサル方法です。
したがって、この走査ではまずルートノードから始まり、レベル0に対応するノード、次にレベル1に対応するノード、そしてそれ以降のノードを順に走査します。
上記の例のバイナリツリーにおいて、レベル順同士を巡回すると次のようになります。
(ルート)10 → 20 → 30 → 40 → 50
これを行うには、2つのことをする必要があります。
-
- まずは木の高さを見つけなければなりません。
- 各レベルに対応するノードを出力する方法を見つける必要があります。
木の高さを測ってください。
まず、木の高さを見つけます。これをするために、論理はシンプルです。
木の高さは、根から葉までの最も長いパスと定義されているため、左の部分木と右の部分木の高さを再帰的に計算し、部分木の最大高さを求めることができます。木の高さは、部分木の高さ + 1となります。
C-スタイルの疑似コード:
// Find height of a tree, defined by the root node
int tree_height(Node* root) {
if (root == NULL)
return 0;
else {
// Find the height of left, right subtrees
left_height = tree_height(root->left);
right_height = tree_height(root->right);
// Find max(subtree_height) + 1 to get the height of the tree
return max(left_height, right_height) + 1;
}
すべてのレベルにおけるすべてのノードを印刷してください。
高さがわかったので、各レベルのノードを表示する必要があります。これを行うために、高さまでのすべてのレベルを反復処理するために for ループを使用し、各レベルでノードを表示します。
void print_tree_level_order(Node* root) {
int height = tree_height(root);
for (int i=0; i<height; i++) {
// Print the ith level
print_level(root, i);
}
}
木のi番目のレベルを表示するために、別の関数が必要であることに注意してください。
ここでも、似たような論理があります。ただし、今回は根ノードを印刷した後、その根ノードを左の子と右の子に変更し、両方のサブツリーを印刷します。
次のステップでは、補助のルートがNULLになると、これは葉ノードに到達するまで続きます(葉ノード->left = NULLかつ葉ノード->right = NULLの場合)。
void print_level(Node* root, int level_no) {
// Prints the nodes in the tree
// having a level = level_no
// We have a auxiliary root node
// for printing the root of every
// sub-tree
if (!root)
return;
if (level_no == 0) {
// We are at the top of a sub-tree
// So print the auxiliary root node
printf("%d -> ", root->value);
}
else {
// Make the auxiliary root node to
// be the left and right nodes for
// the sub-trees and decrease level by 1, since
// you are moving from top to bottom
print_level(root->left, level_no - 1);
print_level(root->right, level_no - 1);
}
}
今、私たちはついにLevel Order Traversalを完成しました!
以下に完全なプログラムを提供します。また、挿入を使用してバイナリツリーを構築するセクションも含まれています。
完成したC/C++コード
元々はCプログラムですが、同じものはC++でもコンパイルできます。
/**
Code for https://scdev.com
File Name: level_order.c
Purpose: Find the Level Order Traversal of a Binary Tree
@author Vijay Ramachandran
@date 28/01/2020
*/
#include <stdio.h>
#include <stdlib.h>
typedef struct Node Node;
// Define the Tree Node here
struct Node {
int value;
// Pointers to the left and right children
Node* left, *right;
};
Node* init_tree(int data) {
// Creates the tree and returns the
// root node
Node* root = (Node*) malloc (sizeof(Node));
root->left = root->right = NULL;
root->value = data;
return root;
}
Node* create_node(int data) {
// Creates a new node
Node* node = (Node*) malloc (sizeof(Node));
node->value = data;
node->left = node->right = NULL;
return node;
}
void free_tree(Node* root) {
// Deallocates memory corresponding
// to every node in the tree.
Node* temp = root;
if (!temp)
return;
free_tree(temp->left);
free_tree(temp->right);
if (!temp->left && !temp->right) {
free(temp);
return;
}
}
int tree_height(Node* root) {
// Get the height of the tree
if (!root)
return 0;
else {
// Find the height of both subtrees
// and use the larger one
int left_height = tree_height(root->left);
int right_height = tree_height(root->right);
if (left_height >= right_height)
return left_height + 1;
else
return right_height + 1;
}
}
void print_level(Node* root, int level_no) {
// Prints the nodes in the tree
// having a level = level_no
// We have a auxiliary root node
// for printing the root of every
// subtree
if (!root)
return;
if (level_no == 0) {
// We are at the top of a subtree
// So print the auxiliary root node
printf("%d -> ", root->value);
}
else {
// Make the auxiliary root node to
// be the left and right nodes for
// the subtrees and decrease level by 1, since
// you are moving from top to bottom
print_level(root->left, level_no - 1);
print_level(root->right, level_no - 1);
}
}
void print_tree_level_order(Node* root) {
if (!root)
return;
int height = tree_height(root);
for (int i=0; i<height; i++) {
printf("Level %d: ", i);
print_level(root, i);
printf("\n");
}
printf("\n\n-----Complete Level Order Traversal:-----\n");
for (int i=0; i<height; i++) {
print_level(root, i);
}
printf("\n");
}
int main() {
// Program to demonstrate Level Order Traversal
// Create the root node having a value of 10
Node* root = init_tree(10);
// Insert nodes onto the tree
root->left = create_node(20);
root->right = create_node(30);
root->left->left = create_node(40);
root->left->right = create_node(50);
// Level Order Traversal
print_tree_level_order(root);
// Free the tree!
free_tree(root);
return 0;
}
結果
Level 0: 10 ->
Level 1: 20 -> 30 ->
Level 2: 40 -> 50 ->
-----Complete Level Order Traversal:-----
10 -> 20 -> 30 -> 40 -> 50 ->
この目的のために私が作成したGithubのgistを通じてこれをダウンロードすることもできます。(挿入のためのコードも含んでいます)
結論
C/C++でレベル順の走査法を実装する方法について、より理解を深めていただければ幸いです。もしご質問がありましたら、下記のコメント欄からお気軽にお尋ねください。

