平衡二分木とは何か、そしてどのように確認するのかを説明してください。

2年 ago

陽, 向宇

2 minutes

バイナリツリーの場合、ツリーが傾いていると、操作を行う際に計算効率が低下します。

この理由から、木が傾かないようにするための動機が生まれます。そのため、バランスの取れた二分木が必要です。

平衡二分木とは何ですか？ (Hēkō nibunki to wa nan desu ka?)

バランス二分木は操作を行う際に計算効率が高いです。

バランスの取れた二分木は、以下の条件に従います。 (Baransu no totta nibun-ki wa, irekae no jouken ni shitagau.)

各ノードにおいて、右部分木はバランスが取れた二分木です。

高さバランスのとれた二進木

平衡二分木は、高さバランス二分木としても知られています。高さバランス二分木は、左側と右側の部分木の高さの差を表すkによってHB(k)と表されます。’k’はバランスファクターとして知られています。

木に対してバランスファクター（k）がゼロであれば、その木は完全にバランスが取れた二分木として知られています。これはHB（0）と表されます。

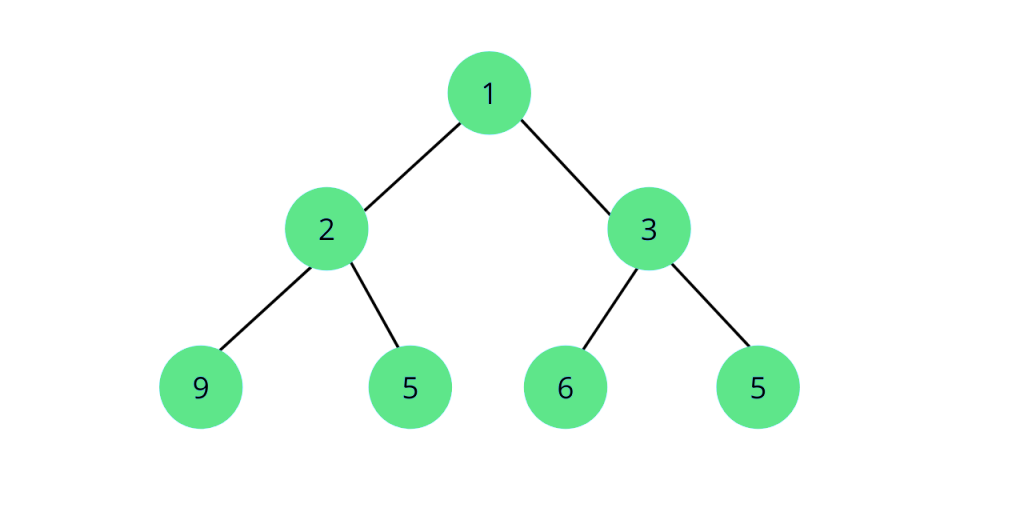
自己バランス二分探索木

二分探索木のバランスファクターが1である場合、それはAVL（アデルソン・ヴェルスキー・ランディス）木です。つまり、AVL木では左部分木と右部分木の高さの差は最大でも1であることを意味します。

AVL木は自己バランス型の二分探索木です。AVL木では、左部分木と右部分木の差が1より大きい場合、以下の4つの回転操作のいずれかを行って自己をバランスさせます。

Left rotation
Right rotation
Left-Right rotation
Right-Left rotation

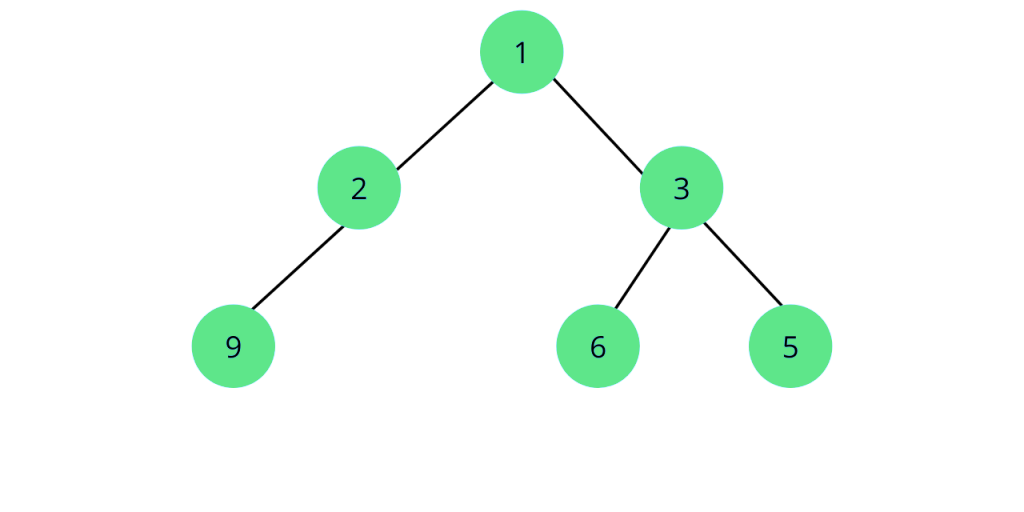
バイナリツリーがバランスしているかどうかをチェックする方法は？

バイナリツリーがバランスしているかを確認するためには、三つの条件をチェックする必要があります。

各ノードにおいて、右のサブツリーはバランスの取れた二分木でなければならない。

樹木の高さを計算できる関数が必要です。これを行う一つの方法は、高さを計算するために別の関数を作成し、必要な都度呼び出すことです。しかし、これは計算的に非効率です。

これを実装するのにより良い方法は、同じ関数内で高さを返すことです。

各ノードについて、そのノード/部分木がバランスしていない場合は-1を返し、バランスしている場合はそのノード/部分木の高さを返します。

アルゴリズムは次のようになります：

If node == null -> return 0
Check left subtree. If not balanced -> return -1
Check right subtree. If not balanced -> return -1
The absolute between heights of left and right subtrees. If it is greater than 1 -> return -1.
If the tree is balanced -> return height

疑似コードは次のようになります。 (Giji kōdo wa tsugi no yōni narimasu.)

 private int balanceHeight (TreeNode currentNode)
    {
        if (currentNode == null)
        {
            return 0;
        }

        // checking left subtree
        int leftSubtreeHeight = balanceHeight (currentNode.left);
        if (leftSubtreeHeight == -1) return -1;
        // if left subtree is not balanced then the entire tree is also not balanced

        //checking right subtree
        int rightSubtreeHeight = balanceHeight (currentNode.right);
        if (rightSubtreeHeight == -1) return -1;
        // if right subtree is not balanced then the entire          tree is also not balanced

        //checking the difference of left and right subtree for current node
        if (Math.abs(leftSubtreeHeight - rightSubtreeHeight) > 1)
        {
            return -1;
        }
        //if it is balanced then return the height
        return (Math.max(leftSubtreeHeight, rightSubtreeHeight) + 1);
    }

この機能は、木のルートで呼び出すことができ、もし-1以外の値が返される場合、それはバランス二分木です。-1が返される場合、バランス二分木ではありません。

結論

このチュートリアルでは、バランス二分木について学び、どのようにして木がバランス二分木であるかを確認することができるかを説明しました。私たちと一緒に学びながら、理解して楽しんでいただけたことを願っています。