最小ヒープの二分木
最小ヒープ二分木とは、根ノードが木内で最小のキーを持つ二分木である。
上記の定義は、木のすべてのサブツリーに当てはまります。これを最小ヒープの特性と呼びます。
最後の2つの層以外のほぼすべてのノードは、2つの子ノードを持っている必要があります。つまり、最後の2つの層を除いて、ほぼ完全な二分木です。
以下の木は、上記の2つの特性が満たされているので、最小ヒープ二分木の例です。
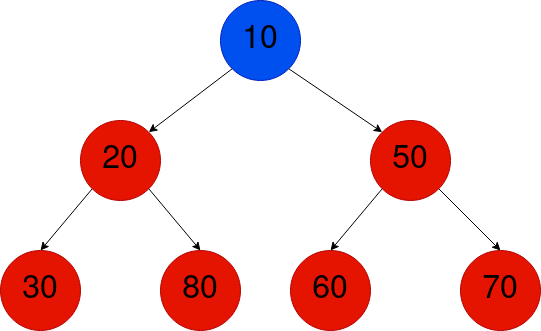
「最小ヒープ木」の概要を説明したので、その表現方法を見てみましょう。
ミンヒープツリーの表現
ミンヒープ二分木は、一般的には以下の形式に従ってインデックス化された配列として表されます。
| Current Node | arr[i] |
| Parent Node | arr[(i-1)/2] |
| Left Child | arr[(2*i) + 1] |
| Right Child | arr[(2*i )+ 2] |
全体の木の根はarr[0]にあります。
下の図に示されているように、私たちはインデックスを使用します。このパターンは非常にわかりやすく、上記の表と一致するでしょう。
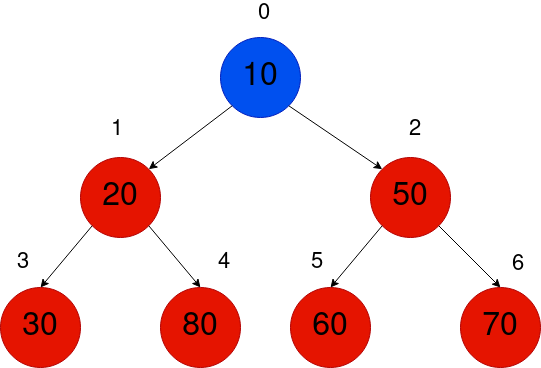
このインデックス付けは、バイナリツリーのレベル順トラバーサルに従いますので、バイナリヒープ配列はレベル順トラバーサルを使用したバイナリツリーです。
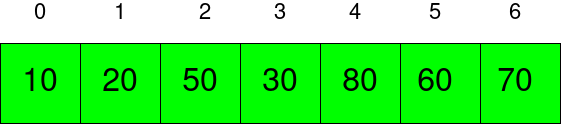
上の図は、最小ヒープツリーの配列表現を示しています。
今の概念をカバーしたので、次はCでの実装に移りましょう。
ミニヒープ木の実装
配列表現を使用して木を構築します。最小ヒープの構造を書き始めましょう。 (Hairetsu hyōgen o shiyō shite ki o kōchiku shimasu. Saishō hīpu no kōzō o kakishidemashou.)
typedef struct MinHeap MinHeap;
struct MinHeap {
int* arr;
// Current Size of the Heap
int size;
// Maximum capacity of the heap
int capacity;
};
私たちは要素の配列とサイズを持ちます。要素が挿入または削除されるとサイズが更新されます。
配列には、最大サイズを示す容量もあります。
ミニヒープ木を表すために、親や子供を見つけるといったいくつかの関数を書く必要があります。
int parent(int i) {
// Get the index of the parent
return (i - 1) / 2;
}
int left_child(int i) {
return (2*i + 1);
}
int right_child(int i) {
return (2*i + 2);
}
int get_min(MinHeap* heap) {
// Return the root node element,
// since that's the minimum, by the min-heap
// property
return heap->arr[0];
}
ヒープを初期化および解放する関数を作成します。
MinHeap* init_minheap(int capacity) {
MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
minheap->arr = (int*) calloc (capacity, sizeof(int));
minheap->capacity = capacity;
minheap->size = 0;
return minheap;
}
void free_minheap(MinHeap* heap) {
if (!heap)
return;
free(heap->arr);
free(heap);
}
それがカバーされたので、では、次に要素を挿入する方法に移りましょう!
Min Heap に挿入する。
挿入アルゴリズムはシンプルです。これは要素を木に挿入します。
アルゴリズムの解説を分かりやすく述べる。
- First, always insert at the bottom of the tree. The initial position of the inserted element is at the last level.
- We will now need to update the position of this element so that the min-heap property is satisfied.
- Since the root node of every sub-tree must be the minimum, check the sub-tree of its immediate parent.
- If the parent is greater than this inserted element, we need to update its position by swapping it.
- But we are not yet done, since the min-heap property may be violated of the updated node’s sub-tree!
- We need to keep swapping until we reach the root node, after which we are done.
この手順を理解するために、例を挙げましょう。 (Kono shorui wo rikai suru tameni, rei wo agemashou.)
下記の木を考えてみてください。要素はただ1つだけです。

エレメント40を挿入しましょう。エレメントが1つだけなので、一番下に挿入され、最小ヒープの性質が満たされていることがわかります。なぜなら10は40よりも小さいからです。だから交換する必要はありません。
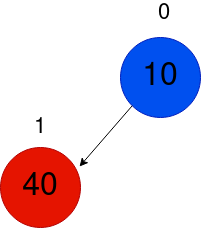
次に、50を挿入します。同様の手続きが続きます。
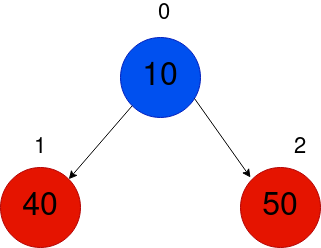
次に、5を挿入します。これで、まずはツリーの一番下に、インデックス3に挿入します。
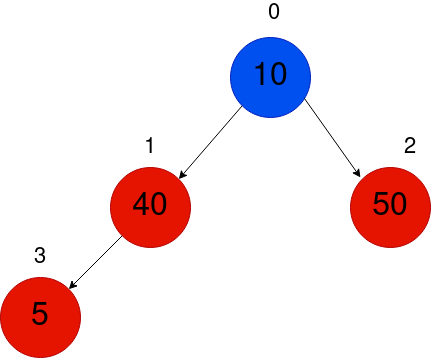
部分木1-3において、最小ヒープの条件が破られているため、全体の木でも同様です。したがって、ルートに到達するまで親と交換し続ける必要があります。
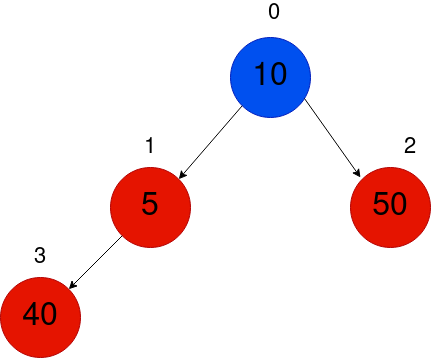
だから、再び0番ノードを根とする部分木で最小ヒープの性質が破られているため、もう1つのスワップが必要です。
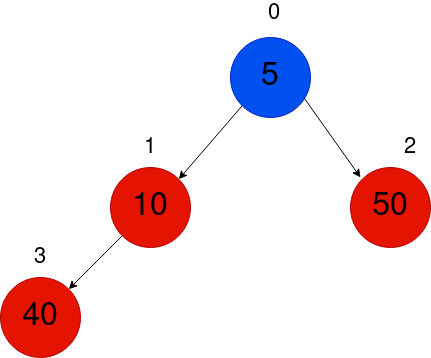
わかりました。イメージができたので、それを書きましょう!(Wakarimashita. Imēji ga dekita node, sore o kakimashou!)
MinHeap* insert_minheap(MinHeap* heap, int element) {
// Inserts an element to the min heap
// We first add it to the bottom (last level)
// of the tree, and keep swapping with it's parent
// if it is lesser than it. We keep doing that until
// we reach the root node. So, we will have inserted the
// element in it's proper position to preserve the min heap property
if (heap->size == heap->capacity) {
fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
return heap;
}
// We can add it. Increase the size and add it to the end
heap->size++;
heap->arr[heap->size - 1] = element;
// Keep swapping until we reach the root
int curr = heap->size - 1;
// As long as you aren't in the root node, and while the
// parent of the last element is greater than it
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
// Swap
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
// Update the current index of element
curr = parent(curr);
}
return heap;
}
今、削除メソッドを実装します。
ミンヒープから削除してください。
私たちは、インデックスのどの要素を削除するかを見る前に、最小ヒープは根と非常に密接に関連しているため、まず根を削除することを考えます。
最小の要素(つまり根)を削除するために、以下の手順を行います。
- Update the root as the last element of the array (tree)
- We will now remove the last element at the bottom. This is similar to swapping and deleting at the end! Only because we don’t care about the root value anymore, we simply update it instead.
- The problem again is that we need to maintain the min-heap property.
- So we must ensure that the whole tree maintains this property. We will use a function called heapify() to do this for us.
ですから、私たちはヒープ化(heapify())メソッドを行った後に、削除方法が完了することを知っています。
MinHeap* delete_minimum(MinHeap* heap) {
// Deletes the minimum element, at the root
if (!heap || heap->size == 0)
return heap;
int size = heap->size;
int last_element = heap->arr[size-1];
// Update root value with the last element
heap->arr[0] = last_element;
// Now remove the last element, by decreasing the size
heap->size--;
size--;
// We need to call heapify(), to maintain the min-heap
// property
heap = heapify(heap, 0);
return heap;
}
ヒープ整理(heapify)手続き
この機能は要素のインデックスindexを受け取り、即時のサブツリーの最小の要素と入れ替えて、最小ヒープの特性を維持します。
得られる木は、最小ヒープの性質を満たします。 (Erareru ki wa, saishō-hīpu no seishitsu o mitashimasu.)
この場合、部分木の最小要素を見つけて、現在の要素と交換することが必要です。
これからは、木全体がこれを満たしていることを確認する必要があります。そのためには、最も小さな要素に対して手順を再帰的に呼び出し、最終的にはルートまで到達する必要があります。
MinHeap* heapify(MinHeap* heap, int index) {
// Rearranges the heap as to maintain
// the min-heap property
if (heap->size <= 1)
return heap;
int left = left_child(index);
int right = right_child(index);
// Variable to get the smallest element of the subtree
// of an element an index
int smallest = index;
// If the left child is smaller than this element, it is
// the smallest
if (left < heap->size && heap->arr[left] < heap->arr[index])
smallest = left;
// Similarly for the right, but we are updating the smallest element
// so that it will definitely give the least element of the subtree
if (right < heap->size && heap->arr[right] < heap->arr[smallest])
smallest = right;
// Now if the current element is not the smallest,
// swap with the current element. The min heap property
// is now satisfied for this subtree. We now need to
// recursively keep doing this until we reach the root node,
// the point at which there will be no change!
if (smallest != index)
{
int temp = heap->arr[index];
heap->arr[index] = heap->arr[smallest];
heap->arr[smallest] = temp;
heap = heapify(heap, smallest);
}
return heap;
}
今、delete_minimum()関数を拡張して、任意の要素を削除できるようにすることができます。
任意の要素を削除する
現在の最小値より小さくなるよう、希望する要素を最小可能値に設定するだけで済みます。それは get_min() – 1 となります。
今から、新しい根がこの要素になるように、位置を更新するまで、入れ替えを続けます。
今、私たちは古いdelete_minimum()関数に戻ってきました!新しい根を簡単に削除することができます!
これにより、私たちの全体の削除手順は次のようになります。
MinHeap* delete_element(MinHeap* heap, int index) {
// Deletes an element, indexed by index
// Ensure that it's lesser than the current root
heap->arr[index] = get_min(heap) - 1;
// Now keep swapping, until we update the tree
int curr = index;
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
curr = parent(curr);
}
// Now simply delete the minimum element
heap = delete_minimum(heap);
return heap;
}
ふぅ!やっと終わりました。今から、これまでのコードとprint()関数を使って、ツリーを視覚化します。
完全なコード
#include <stdio.h>
#include <stdlib.h>
typedef struct MinHeap MinHeap;
struct MinHeap {
int* arr;
// Current Size of the Heap
int size;
// Maximum capacity of the heap
int capacity;
};
int parent(int i) {
// Get the index of the parent
return (i - 1) / 2;
}
int left_child(int i) {
return (2*i + 1);
}
int right_child(int i) {
return (2*i + 2);
}
int get_min(MinHeap* heap) {
// Return the root node element,
// since that's the minimum
return heap->arr[0];
}
MinHeap* init_minheap(int capacity) {
MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
minheap->arr = (int*) calloc (capacity, sizeof(int));
minheap->capacity = capacity;
minheap->size = 0;
return minheap;
}
MinHeap* insert_minheap(MinHeap* heap, int element) {
// Inserts an element to the min heap
// We first add it to the bottom (last level)
// of the tree, and keep swapping with it's parent
// if it is lesser than it. We keep doing that until
// we reach the root node. So, we will have inserted the
// element in it's proper position to preserve the min heap property
if (heap->size == heap->capacity) {
fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
return heap;
}
// We can add it. Increase the size and add it to the end
heap->size++;
heap->arr[heap->size - 1] = element;
// Keep swapping until we reach the root
int curr = heap->size - 1;
// As long as you aren't in the root node, and while the
// parent of the last element is greater than it
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
// Swap
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
// Update the current index of element
curr = parent(curr);
}
return heap;
}
MinHeap* heapify(MinHeap* heap, int index) {
// Rearranges the heap as to maintain
// the min-heap property
if (heap->size <= 1)
return heap;
int left = left_child(index);
int right = right_child(index);
// Variable to get the smallest element of the subtree
// of an element an index
int smallest = index;
// If the left child is smaller than this element, it is
// the smallest
if (left < heap->size && heap->arr[left] < heap->arr[index])
smallest = left;
// Similarly for the right, but we are updating the smallest element
// so that it will definitely give the least element of the subtree
if (right < heap->size && heap->arr[right] < heap->arr[smallest])
smallest = right;
// Now if the current element is not the smallest,
// swap with the current element. The min heap property
// is now satisfied for this subtree. We now need to
// recursively keep doing this until we reach the root node,
// the point at which there will be no change!
if (smallest != index)
{
int temp = heap->arr[index];
heap->arr[index] = heap->arr[smallest];
heap->arr[smallest] = temp;
heap = heapify(heap, smallest);
}
return heap;
}
MinHeap* delete_minimum(MinHeap* heap) {
// Deletes the minimum element, at the root
if (!heap || heap->size == 0)
return heap;
int size = heap->size;
int last_element = heap->arr[size-1];
// Update root value with the last element
heap->arr[0] = last_element;
// Now remove the last element, by decreasing the size
heap->size--;
size--;
// We need to call heapify(), to maintain the min-heap
// property
heap = heapify(heap, 0);
return heap;
}
MinHeap* delete_element(MinHeap* heap, int index) {
// Deletes an element, indexed by index
// Ensure that it's lesser than the current root
heap->arr[index] = get_min(heap) - 1;
// Now keep swapping, until we update the tree
int curr = index;
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
curr = parent(curr);
}
// Now simply delete the minimum element
heap = delete_minimum(heap);
return heap;
}
void print_heap(MinHeap* heap) {
// Simply print the array. This is an
// inorder traversal of the tree
printf("Min Heap:\n");
for (int i=0; i<heap->size; i++) {
printf("%d -> ", heap->arr[i]);
}
printf("\n");
}
void free_minheap(MinHeap* heap) {
if (!heap)
return;
free(heap->arr);
free(heap);
}
int main() {
// Capacity of 10 elements
MinHeap* heap = init_minheap(10);
insert_minheap(heap, 40);
insert_minheap(heap, 50);
insert_minheap(heap, 5);
print_heap(heap);
// Delete the heap->arr[1] (50)
delete_element(heap, 1);
print_heap(heap);
free_minheap(heap);
return 0;
}
出力
Min Heap:
5 -> 50 -> 40 ->
Min Heap:
5 -> 40 ->
実装の時間計算量
上記の手続きの時間の複雑さは以下の通りです。
| Function | Time Complexity |
get_min() |
O(1) |
insert_minheap() |
O(logN) |
delete_minimum() |
Same as insert – O(logN) |
heapify() |
O(logN) |
delete_element() |
O(logN) |
コードをダウンロードしてください。
私がアップロードしたGithub Gistから完全なコードをダウンロードすることができます。何か質問がありましたら、以下のコメントセクションでお尋ねください!
結論
この記事では、Min Heapバイナリツリーをどのように表現できるかを学び、Cでの実装も見ていきました。
参考文献
- An illustration of Heaps, from Cormen
- Wikipedia article on Binary Heaps

