Javaでの最大ヒープデータ構造の実装
最大ヒープは、あるノードの値がその子ノードの値以上である完全二分木です。最大ヒープのデータ構造は、ヒープソートを用いてデータをソートする際に役立ちます。
このチュートリアルでは、Javaで最大ヒープをスクラッチから実装するために必要なすべてのことをカバーします。
Javaでの最大ヒープデータ構造の実装
私たちは配列を使用してヒープを表現します。ヒープは完全二分木であるため、スペースの浪費はありません。
例えば、次のようなヒープを考えてみましょう:
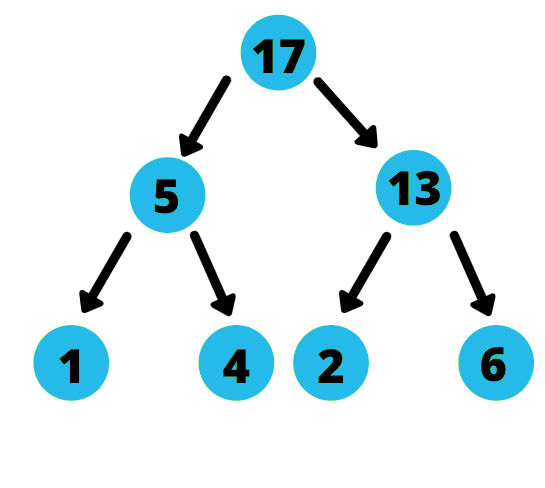
配列の表現は次の通りです。
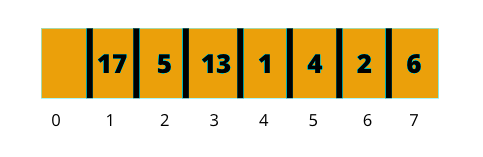
最大ヒープの宣言は次のように行われます。
static class MaxHeap {
private int[] Heap; // array
private int size;
private int maxsize;
public MaxHeap(int size) {
this.maxsize = size;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MAX_VALUE;
}
ヒープは、最大ヒープを格納する配列です。コンストラクタはサイズを受け取り、配列を無限大の0番目の要素で初期化します。ヒープはインデックス1から始めます。
1. ノードの親を取得する (Nōdo no oyako o shutoku suru)
私たちはヒープを配列として保存しているため、ノードの親を取得することが容易になります。
要素iの親の位置は次のように与えられます:
(i)/2
実装中は、次の方法で親を取得することができます:
private int parent(int pos) {
return pos / 2;
}
2.ノードに子供を取得する
位置iにあるノードの子ノードは以下の式で与えられます。
左の子供: 左側の子供
(2*i)
右の子供 : Migi no kodomo
(2*i)+ 1
注意:ヒープのインデックスが1から始まる場合に限り、左の子ノードと右の子ノードの値はそれぞれ(2*i) + 1と(2*i) + 2となります。
コードでは、次のように実装します。
private int leftChild(int pos) {
return (2 * pos) ;
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
3.新しく挿入された要素をヒープ化する。
要素をヒープに挿入した後、ヒープの性質が満たされない場合があります。その場合、ヒープの位置を調整して再びヒープにする必要があります。このプロセスはヒープ化と呼ばれています。
最大ヒープで要素をヒープ化するには、その子要素の中で最大値を見つけ、現在の要素と入れ替える必要があります。このプロセスを、各ノードにおいてヒープの性質が満たされるまで繰り返します。
ヒープソートを行うために、ルートから葉まで下へ移動します。したがって、これは「ダウンヒープソート」とも呼ばれています。
もう一つの興味深い点は、ダウンヒープファイを非葉ノードのみに実行することです。
ダウンヒープ関数のコードは次のとおりです。
private void downHeapify(int pos) {
//checking if the node is a leaf node
if (pos >= (size / 2) && pos <= size)
return;
//checking if a swap is needed
if (Heap[pos] < Heap[leftChild(pos)] ||
Heap[pos] < Heap[rightChild(pos)]) {
//replacing parent with maximum of left and right child
if (Heap[leftChild(pos)] > Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
//after swaping, heapify is called on the children
downHeapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
//after swaping, heapify is called on the children
downHeapify(rightChild(pos));
}
}
}
スワップ関数は以下のようになります。
private void swap(int fpos, int spos) {
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
再帰ではなく、whileループを使って同じコードを書くこともできます。
ダウンヒープ法では、私たちは親から子へと移動していました。同様に、ボトムアップの方法でも移動することができます。ボトムアップの方法で移動するときは、ノードをその親と比較します。これはアップヒープ法と呼ばれます。
アップヒープ化のコードは次の通りです。
private void heapifyUp(int pos) {
int temp = Heap[pos];
while(pos>0 && temp > Heap[parent(pos)]){
Heap[pos] = Heap[parent(pos)];
pos = parent(pos);
}
Heap[pos] = temp;
}
私たちは再帰の代わりに、whileループを使用してup_heapifyのコードを書きました。
4. 新しいノードを挿入します。 (Atarashii nodō o sōnyū shimasu.)
配列の末尾に新しい要素が追加され、ヒープの特性が保持されるようにスワップが行われます。
挿入のアルゴリズムは次のようになります。
-
- ヒープサイズを増やす
-
- 新しい要素をヒープの最後に置く
- 下から上へヒープ化する
挿入のためのコードは以下の通りです:
public void insert(int element) {
Heap[++size] = element;
int current = size;
heapifyUp(current);
}
5. ノードの削除/抽出
ヒープからノードを削除/抽出するために、ルートから要素を削除します。ルートは常に最大の要素を返します。
削除のアルゴリズムは以下の通りです。
-
- 最初の要素を変数にコピーする。
-
- 最後の要素を最初の位置(ルート)にコピーする。
- downHeapify() を呼び出す。
削除のためのコードは:
public int extractMax() {
int max = Heap[1];
Heap[1] = Heap[size--];
downHeapify(1);
return max;
}
ここではサイズを小さくするために、サイズ−−を使用してヒープのサイズを減らします。
JavaでのMax Heapの完全実装
完全なJava実装のMax Heapは次のようになります。
package com.JournalDev;
public class Main {
static class MaxHeap {
private int[] Heap;
private int size;
private int maxsize;
public MaxHeap(int size) {
this.maxsize = size;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MAX_VALUE;
}
private int parent(int pos) {
return pos / 2;
}
private int leftChild(int pos) {
return (2 * pos) ;
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
private void swap(int fpos, int spos) {
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
private void downHeapify(int pos) {
if (pos >= (size / 2) && pos <= size)
return;
if (Heap[pos] < Heap[leftChild(pos)] ||
Heap[pos] < Heap[rightChild(pos)]) {
if (Heap[leftChild(pos)] > Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
downHeapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
downHeapify(rightChild(pos));
}
}
}
private void heapifyUp(int pos) {
int temp = Heap[pos];
while(pos>0 && temp > Heap[parent(pos)]){
Heap[pos] = Heap[parent(pos)];
pos = parent(pos);
}
Heap[pos] = temp;
}
public void insert(int element) {
Heap[++size] = element;
int current = size;
heapifyUp(current);
}
public void print() {
for (int i = 1; i <= size / 2; i++) {
System.out.print(+ Heap[i] + ": L- " +
Heap[2 * i] + " R- " + Heap[2 * i + 1]);
System.out.println();
}
}
public int extractMax() {
int max = Heap[1];
Heap[1] = Heap[size--];
downHeapify(1);
return max;
}
}
public static void main(String[] arg)
{
MaxHeap maxHeap = new MaxHeap(15);
maxHeap.insert(1);
maxHeap.insert(4);
maxHeap.insert(2);
maxHeap.insert(5);
maxHeap.insert(13);
maxHeap.insert(6);
maxHeap.insert(17);
maxHeap.print();
System.out.println("The max is " + maxHeap.extractMax());
}
}
Output :
17: L- 5 R- 13
5: L- 1 R- 4
13: L- 2 R- 6
The max is 17
結論
このチュートリアルは、JavaでのMaxヒープデータ構造についてでした。

