C / C++におけるトライデータ構造
Trie(トライ)データ構造は、動的配列のコンテナとして機能します。この記事では、C/C++でTrieを実装する方法を見ていきます。
これは木のデータ構造に基づいていますが、必ずしもキーを保存するわけではありません。ここでは、各ノードには値のみがあり、その値は位置に基づいて定義されます。
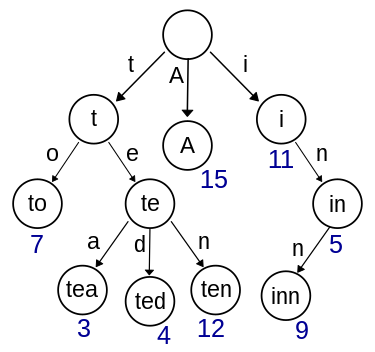
それぞれのノードの値は、一連のマッチの後の根ノードからの接頭辞を示します。
私たちはそのような一致を接頭辞の一致と呼んでいます。したがって、トライを使って辞書の単語を保存することができます!
例えば、上記の図において、根ノードは空であるため、どんな文字列も根ノードに一致します。ノード7はtoの接頭辞文字列に一致し、ノード3はteaの接頭辞文字列に一致します。
ここでは、キーは葉ノードの位置にだけ保存されます。接頭辞一致は葉ノードで止まるため、非葉ノードは文字列全体ではなく、接頭辞に一致する文字だけを保存します。
これらの理由から、トライはプレフィックスツリーと呼ばれています。では、プログラマの観点からこのデータ構造をどのように実装できるかを理解しましょう。
C/C++でトライデータ構造を実装する
まず、トライ構造を書きましょう。トライノードには特に2つの要素があります。
- It’s children
- A marker to indicate a leaf node.
ただし、Trieも印刷する予定ですので、データ部にもう1つ属性を保存できれば、より簡単になります。
では、TrieNodeの構造を定義しましょう。ここでは、小文字のアルファベットのみを格納するため、これを26分木として実装します。したがって、各ノードには26個の子ノードへのポインタがあります。
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
私たちが構造を定義したので、メモリ内にTrieNodeを初期化するための関数と、そのポインタを解放するための関数を書きましょう。
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
Trieに単語を挿入する
今、insert_trie()関数を書きます。この関数は、ルートノード(最上位ノード)へのポインタを受け取り、Trieに単語を挿入します。
挿入手続きは簡単です。単語を文字ごとに繰り返し処理し、相対位置を評価します。
たとえば、bという文字の位置は1であり、それは2番目の子供となります。
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
プレフィックスを一文字ずつ比較し、存在しない場合は単にノードを初期化します。
それ以外の場合、私たちは単純にチェーンを下に移動し続けて、全ての文字にマッチするまで進みます。
temp = temp->children[idx];
最後に、すべての一致しない文字を挿入し、更新されたトライを返します。
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
トライ木構造内で単語を検索してください。
トライに挿入を実装したので、与えられたパターンの検索を見てみましょう。
上記と同じプレフィックスマッチング戦略を使用し、文字列を文字ごとに一致させようとします。
もし私たちがチェーンの終わりに到達し、まだ一致するものを見つけていない場合、それは文字列が存在しないことを意味します。完全なプレフィックスの一致が行われていないためです。
この条件が正しく返されるためには、私たちのパターンが完全に一致し、マッチングが終了した後に葉ノードに到達する必要があります。
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
わかりました。挿入と検索の手続きは完了しました。
テストするために、まずprint_tree()関数を書きます。この関数は、すべてのノードのデータを表示します。
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
今、それをやり終えたので、これまでの完全なプログラムを実行して、正しく動作しているか確認しましょう。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
void print_search(TrieNode* root, char* word) {
printf("Searching for %s: ", word);
if (search_trie(root, word) == 0)
printf("Not Found\n");
else
printf("Found!\n");
}
int main() {
// Driver program for the Trie Data Structure Operations
TrieNode* root = make_trienode('\0');
root = insert_trie(root, "hello");
root = insert_trie(root, "hi");
root = insert_trie(root, "teabag");
root = insert_trie(root, "teacan");
print_search(root, "tea");
print_search(root, "teabag");
print_search(root, "teacan");
print_search(root, "hi");
print_search(root, "hey");
print_search(root, "hello");
print_trie(root);
free_trienode(root);
return 0;
}
あなたのGCCコンパイラでコンパイル後、以下の出力が得られます。
Searching for tea: Not Found
Searching for teabag: Found!
Searching for teacan: Found!
Searching for hi: Found!
Searching for hey: Not Found
Searching for hello: Found!
-> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
print_tree()メソッドを見ると、どのように印刷されているかが明らかになります。現在のノード、そしてその子ノード全てを印刷するため、順序が示されています。
では、今、削除メソッドを実装しましょう!
Trieから単語を削除してください。
これは実際には他の2つの方法よりも少し複雑です。
キーと値を保存する明示的な方法がないため、特定の形式のアルゴリズムは存在しません。
ただし、この記事の目的に沿って、削除する対象の単語は葉ノードの場合に限定します。つまり、葉ノードまでのプレフィックスマッチングが完全に一致している必要があります。
では始めましょう。削除機能のシグネチャは次のようになります:
TrieNode* delete_trie(TrieNode* root, char* word);
前述したように、葉ノードまでの接頭辞が一致する場合のみ削除されます。したがって、is_leaf_node() という別の関数を作成しましょう。この関数は、私たちのためにそれを行います。
int is_leaf_node(TrieNode* root, char* word) {
// Checks if the prefix match of word and root
// is a leaf node
TrieNode* temp = root;
for (int i=0; word[i]; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
temp = temp->children[position];
}
}
return temp->is_leaf;
}
よし、それで終わったので、delete_trie()メソッドのドラフトを見てみましょう。
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
// TODO
}
このチェックが完了した後、私たちは今、私たちの単語が葉ノードで終わることを知っています。
しかし、対応するべきもう一つの状況があります。もし現在の文字列に部分的な接頭辞が一致する別の単語が存在する場合、どうしますか。
例えば、以下のTrieにおいて、単語「tea」と「ted」は、「te」まで共通の部分があります。
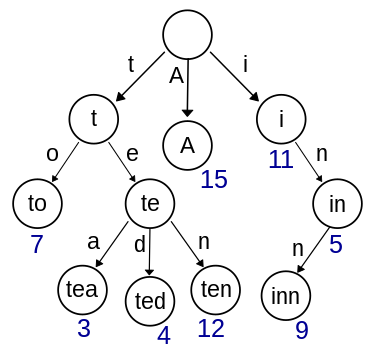
それなら、もしこのようなことが起こった場合、tからaまでの全てのシーケンスを単純に削除することはできません。なぜなら、それらのチェーンはリンクされているため、両方が削除されてしまうからです!
そのため、そのようなマッチが起こる最も深いポイントを見つける必要があります。それ以降に、残りの連鎖を削除することができます。
これには、最も長い接頭辞文字列を見つける必要があるので、別の関数を書きましょう。
char* longest_prefix(TrieNode* root, char* word);
トライにおいて、現在の単語(word)ではない最長のマッチを返します。以下のコードでは、各中間ステップがコメントで説明されています。
char* find_longest_prefix(TrieNode* root, char* word) {
// Finds the longest common prefix substring of word
// in the Trie
if (!word || word[0] == '\0')
return NULL;
// Length of the longest prefix
int len = strlen(word);
// We initially set the longest prefix as the word itself,
// and try to back-track from the deepest position to
// a point of divergence, if it exists
char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
for (int i=0; word[i] != '\0'; i++)
longest_prefix[i] = word[i];
longest_prefix[len] = '\0';
// If there is no branching from the root, this
// means that we're matching the original string!
// This is not what we want!
int branch_idx = check_divergence(root, longest_prefix) - 1;
if (branch_idx >= 0) {
// There is branching, We must update the position
// to the longest match and update the longest prefix
// by the branch index length
longest_prefix[branch_idx] = '\0';
longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
}
return longest_prefix;
}
ここにはもう1つのひねりがあります!最長の一致を見つけるため、アルゴリズムは実際には元の文字列自体と貪欲に一致させようとします!これは望んでいる結果ではありません。
入力文字列とは異なる最も長いマッチを求めますので、別のメソッドであるcheck_divergence()とのチェックが必要です。
現在位置から根までの分岐があるかどうかをチェックし、入力とは異なる最適なマッチの長さを返します。
もし私たちが悪い連鎖にいる場合、それは元の文字列に対応しており、その地点から分岐は起こりません!だから、check_divergence()を使用することで、私たちはその嫌な地点を避ける良い方法です。
int check_divergence(TrieNode* root, char* word) {
// Checks if there is branching at the last character of word
//and returns the largest position in the word where branching occurs
TrieNode* temp = root;
int len = strlen(word);
if (len == 0)
return 0;
// We will return the largest index where branching occurs
int last_index = 0;
for (int i=0; i < len; i++) {
int position = word[i] - 'a';
if (temp->children[position]) {
// If a child exists at that position
// we will check if there exists any other child
// so that branching occurs
for (int j=0; j<N; j++) {
if (j != position && temp->children[j]) {
// We've found another child! This is a branch.
// Update the branch position
last_index = i + 1;
break;
}
}
// Go to the next child in the sequence
temp = temp->children[position];
}
}
return last_index;
}
最後に、私たちはただ無批判に全ての連鎖を削除するのではなく、確認を行いました。だから、今は削除の方法に進みましょう。
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
TrieNode* temp = root;
// Find the longest prefix string that is not the current word
char* longest_prefix = find_longest_prefix(root, word);
//printf("Longest Prefix = %s\n", longest_prefix);
if (longest_prefix[0] == '\0') {
free(longest_prefix);
return root;
}
// Keep track of position in the Trie
int i;
for (i=0; longest_prefix[i] != '\0'; i++) {
int position = (int) longest_prefix[i] - 'a';
if (temp->children[position] != NULL) {
// Keep moving to the deepest node in the common prefix
temp = temp->children[position];
}
else {
// There is no such node. Simply return.
free(longest_prefix);
return root;
}
}
// Now, we have reached the deepest common node between
// the two strings. We need to delete the sequence
// corresponding to word
int len = strlen(word);
for (; i < len; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
// Delete the remaining sequence
TrieNode* rm_node = temp->children[position];
temp->children[position] = NULL;
free_trienode(rm_node);
}
}
free(longest_prefix);
return root;
}
上記のコードは、単にプレフィックスに一致する最も深いノードを検索し、その後に残るシーケンスに一致する単語をTrieから削除します。これは他の一致には関係なく独立して行われます。
上記手続きの時間複雑度
以下に手続きの時間計算量が記載されています。
| Procedure | Time Complexity of Implementation |
search_trie() |
O(n) -> n is the length of the input string |
insert_trie() |
O(n) -> n is the length of the input string |
delete_trie() |
O(C*n) -> C is the number of alphabets, |
| n is the length of the input word |
ほとんどの場合、アルファベットの数は一定なので、delete_trie()の複雑さもO(n)に減少します。
トライデータ構造のための完全なC/C++プログラム。
とうとう(おそらく)delete_trie()関数を完成させました。書いたものが正しいかどうか、ドライバープログラムを使用して確認しましょう。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
int check_divergence(TrieNode* root, char* word) {
// Checks if there is branching at the last character of word
// and returns the largest position in the word where branching occurs
TrieNode* temp = root;
int len = strlen(word);
if (len == 0)
return 0;
// We will return the largest index where branching occurs
int last_index = 0;
for (int i=0; i < len; i++) {
int position = word[i] - 'a';
if (temp->children[position]) {
// If a child exists at that position
// we will check if there exists any other child
// so that branching occurs
for (int j=0; j<N; j++) {
if (j != position && temp->children[j]) {
// We've found another child! This is a branch.
// Update the branch position
last_index = i + 1;
break;
}
}
// Go to the next child in the sequence
temp = temp->children[position];
}
}
return last_index;
}
char* find_longest_prefix(TrieNode* root, char* word) {
// Finds the longest common prefix substring of word
// in the Trie
if (!word || word[0] == '\0')
return NULL;
// Length of the longest prefix
int len = strlen(word);
// We initially set the longest prefix as the word itself,
// and try to back-tracking from the deepst position to
// a point of divergence, if it exists
char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
for (int i=0; word[i] != '\0'; i++)
longest_prefix[i] = word[i];
longest_prefix[len] = '\0';
// If there is no branching from the root, this
// means that we're matching the original string!
// This is not what we want!
int branch_idx = check_divergence(root, longest_prefix) - 1;
if (branch_idx >= 0) {
// There is branching, We must update the position
// to the longest match and update the longest prefix
// by the branch index length
longest_prefix[branch_idx] = '\0';
longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
}
return longest_prefix;
}
int is_leaf_node(TrieNode* root, char* word) {
// Checks if the prefix match of word and root
// is a leaf node
TrieNode* temp = root;
for (int i=0; word[i]; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
temp = temp->children[position];
}
}
return temp->is_leaf;
}
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
TrieNode* temp = root;
// Find the longest prefix string that is not the current word
char* longest_prefix = find_longest_prefix(root, word);
//printf("Longest Prefix = %s\n", longest_prefix);
if (longest_prefix[0] == '\0') {
free(longest_prefix);
return root;
}
// Keep track of position in the Trie
int i;
for (i=0; longest_prefix[i] != '\0'; i++) {
int position = (int) longest_prefix[i] - 'a';
if (temp->children[position] != NULL) {
// Keep moving to the deepest node in the common prefix
temp = temp->children[position];
}
else {
// There is no such node. Simply return.
free(longest_prefix);
return root;
}
}
// Now, we have reached the deepest common node between
// the two strings. We need to delete the sequence
// corresponding to word
int len = strlen(word);
for (; i < len; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
// Delete the remaining sequence
TrieNode* rm_node = temp->children[position];
temp->children[position] = NULL;
free_trienode(rm_node);
}
}
free(longest_prefix);
return root;
}
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
void print_search(TrieNode* root, char* word) {
printf("Searching for %s: ", word);
if (search_trie(root, word) == 0)
printf("Not Found\n");
else
printf("Found!\n");
}
int main() {
// Driver program for the Trie Data Structure Operations
TrieNode* root = make_trienode('\0');
root = insert_trie(root, "hello");
root = insert_trie(root, "hi");
root = insert_trie(root, "teabag");
root = insert_trie(root, "teacan");
print_search(root, "tea");
print_search(root, "teabag");
print_search(root, "teacan");
print_search(root, "hi");
print_search(root, "hey");
print_search(root, "hello");
print_trie(root);
printf("\n");
root = delete_trie(root, "hello");
printf("After deleting 'hello'...\n");
print_trie(root);
printf("\n");
root = delete_trie(root, "teacan");
printf("After deleting 'teacan'...\n");
print_trie(root);
printf("\n");
free_trienode(root);
return 0;
}
結果
Searching for tea: Not Found
Searching for teabag: Found!
Searching for teacan: Found!
Searching for hi: Found!
Searching for hey: Not Found
Searching for hello: Found!
-> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
After deleting 'hello'...
-> h -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
After deleting 'teacan'...
-> h -> i -> t -> e -> a -> b -> a -> g ->
それによって、C / C ++での私たちのTrieデータ構造の実装の終わりに来ました。これは長い文章ですが、これらのメソッドを正しく適用する方法が理解できたことを願っています。
コードをダウンロードしてください。
私がアップロードしたGithub Gistに、完全なコードがあります。効率的なコードではないかもしれませんが、正しく動作するように最善を尽くしました。
もし質問や提案があれば、コメント欄でお知らせください!
参考文献 (さんこうぶんけん)
- Wikipedia Article on Tries
おすすめの読み物:
もし同じようなトピックに興味があるなら、ハッシュテーブルやグラフ理論などのトピックを含む「データ構造とアルゴリズム」セクションを参照してください。

