C/C++における二分木の高さ

二分木の高さとは、ルートノードから任意のリーフノードまでの最長パスの長さであり、つまり、ルートノードから最も奥のリーフノードまでの最短距離ということです。

以下のバイナリツリーを考えてみましょう。

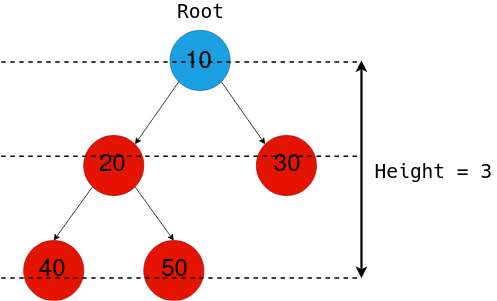
最大の深さに対応する葉のノードが40と50であるため、高さを求めるためには単純に根ノードからこれらのノードのいずれかまでのエッジの数を3で求めればよいです。

二分木の高さがどのような意味を持つかわかったので、今度は任意の二分木の高さを求めるアルゴリズムを構築します。

C++における二分木の高さを求めるための論理

高さを求めるためのロジックを決定し、まずは擬似コードを書きましょう。

ツリー上で再帰を利用して、高さを求めます。（概念についてはWikipediaの記事を参照）

木の高さは、根から葉までの最長のパスとして定義されているため、左の部分木と右の部分木の高さを再帰的に計算することができます。

私たちは今、部分木の高さの定義を適用することができます。

左部分木と右部分木の間で最大値を観察し、その後に1を加える。

木の高さは、部分木の最大の高さに1を加えたものであり、部分木がNULLになり、高さが0になるまで、この操作を繰り返します。

この時点で、私たちの機能はついに終了します。

樹木の高さを計算する関数tree_height()を作成しましょう。

// Find height of a tree, defined by the root node
int tree_height(Node* root) {
    if (root == NULL) 
        return 0;
    else {
        // Find the height of left, right subtrees
        left_height = tree_height(root->left);
        right_height = tree_height(root->right);
         
        // Find max(subtree_height) + 1 to get the height of the tree
        return max(left_height, right_height) + 1;
}

3行目は、サブツリーのサイズが0であるか、またはルートノードがNULLである場合に終了条件を評価します。

7行目と8行目は、左と右の部分木の高さを再帰的に見つけます。

最後に、Line 11は2つの中で最大値を返し、木の高さを返します。

C/C++による実装

以下は、バイナリツリーを構築する完全なプログラムであり、tree_height()関数でツリーの高さを見つけるロジックも示しています。

#include <stdio.h>
#include <stdlib.h>

typedef struct Node Node;

// Define the Tree Node here
struct Node {
    int value;
    // Pointers to the left and right children
    Node* left, *right;
};


Node* init_tree(int data) {
    // Creates the tree and returns the
    // root node
    Node* root = (Node*) malloc (sizeof(Node));
    root->left = root->right = NULL;
    root->value = data;
    return root;
}

Node* create_node(int data) {
    // Creates a new node
    Node* node = (Node*) malloc (sizeof(Node));
    node->value = data;
    node->left = node->right = NULL;
    return node;
}

void free_tree(Node* root) {
    // Deallocates memory corresponding
    // to every node in the tree.
    Node* temp = root;
    if (!temp)
        return;
    free_tree(temp->left);
    free_tree(temp->right);
    if (!temp->left && !temp->right) {
        free(temp);
        return;
    }
}

int tree_height(Node* root) {
    // Get the height of the tree
    if (!root)
        return 0;
    else {
        // Find the height of both subtrees
        // and use the larger one
        int left_height = tree_height(root->left);
        int right_height = tree_height(root->right);
        if (left_height >= right_height)
            return left_height + 1;
        else
            return right_height + 1;
    }
}

int main() {
    // Program to demonstrate finding the height of a Binary Tree

    // Create the root node having a value of 10
    Node* root = init_tree(10);
    
    // Insert nodes onto the tree
    root->left = create_node(20);
    root->right = create_node(30);
    root->left->left = create_node(40);
    root->left->right = create_node(50);

    // Find the height of the tree
    int height = tree_height(root);
    printf("Height of the Binary Tree: %d\n", height);

    // Free the tree!
    free_tree(root);
    return 0;
}