Java/C++でバックトラッキングを使用したN-Queens問題
もし将棋が好きなら、N-クイーン問題を学ぶことは楽しいでしょう。これはバックトラックを理解するのに適した問題です。
バックトラッキングとは何ですか?
バックトラッキングでは、多くの可能な手のうちの1つから始めます。その後、問題を解決しようとします。
選択した手法で問題を解決できるなら、その解答を出力します。そうでなければ、バックトラックして他の手法を選択し、解決を試みます。
もし全ての手がうまくいかなかった場合、私たちはその問題に対する解決策が存在しないと主張します。
N-Queens Problemとは何ですか?
How can N queens be placed on an NxN chessboard so that no two of them attack each other?
この問題は、通常、N=4とN=8の場合によく見られます。
N=4の例を見てみましょう。 (N=よんのれいをみてみましょう。)
チェスのクイーンの動きについて理解する前に、問題を解決する必要があります。
クイーンは、どの方向でも何歩でも動くことができます。ただし、移動中に方向を変えることはできません。
クイーンの動きを見ると、明らかなことは二つのクイーンが同じ行または列に存在することはないということです。
私達は、各行と各列にそれぞれ1つのクイーンを置くことが可能です。
Nが4の時、解は以下のように見えます。
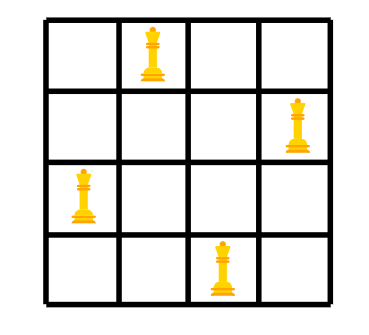
しかし、この配置をどのように取得しますか? (Shikashi, kono haichi o donoyōni shutoku shimasu ka?)
N-Queens問題の解決策
私たちがこの問題を解決しようとする方法は、クイーンをある位置に配置して、その位置が攻撃される可能性を除外しようとすることです。私たちは各行/列に1つのクイーンを配置します。
もし、私たちが女王が選んだ位置で攻撃を受けていることを見つけた場合、私たちは次の位置を試してみます。
クイーンがすべての位置で攻撃されている場合、私たちはバックトラックし、現在の位置より前に配置されたクイーンの位置を変更します。
私たちは、クイーンを配置し、バックトラックするというプロセスを、N個のクイーンがすべて正常に配置されるまで繰り返します。
以下のように、ステップバイステップのバックトラッキングが表示されます。
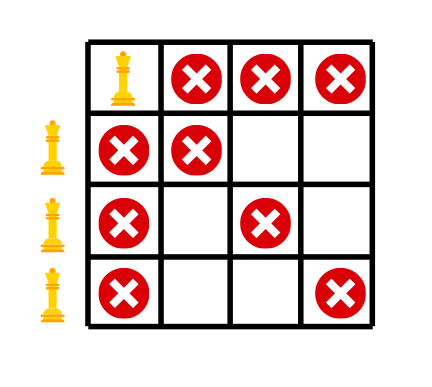
クイーンによって攻撃されている位置に赤い十字印がついています。クイーンを配置する場所が必要ですが、行全体が攻撃されている状態になったら、バックトラックします。
この問題への唯一の解決策ではありません。もしクイーンを時計回りに一歩ずつ動かすと、別の解が得られます。
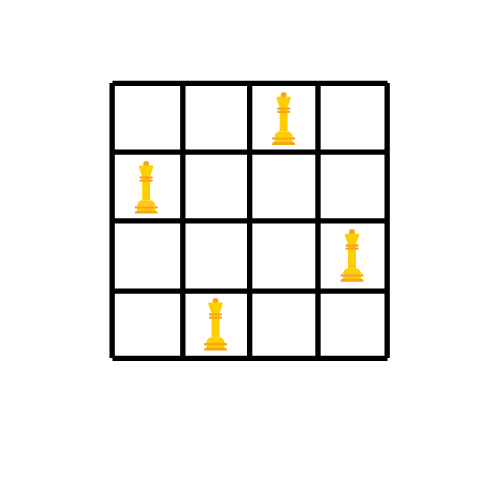
この例では、私たちはクイーンを行に配置しましたが、同様のことを列に関しても行うことができます。その場合、各クイーンは列に属することになります。
C++とJavaにおけるN-Queens問題の実装
C++においてN-Queens問題を実装する。
#define N 4
#include <stdbool.h>
#include <stdio.h>
//function to print the solution
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
printf(" %d ", board[i][j]);
printf("\n");
}
}
// function to check whether the position is safe or not
bool isSafe(int board[N][N], int row, int col)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row][i])
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j])
return false;
return true;
}
// The function that solves the problem using backtracking
bool solveNQUtil(int board[N][N], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
//if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQUtil(board, col + 1))
return true;
//backtrack if the above condition is false
board[i][col] = 0; // BACKTRACK
}
}
return false;
}
// driver program to test above function
int main()
{
int board[N][N] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
printf("Solution does not exist");
return 0;
}
printSolution(board);
return true;
return 0;
}
JavaでN-queens問題の実装
package com.JournalDev;
public class Main {
static final int N = 4;
// print the final solution matrix
static void printSolution(int board[][])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
System.out.print(" " + board[i][j]
+ " ");
System.out.println();
}
}
// function to check whether the position is safe or not
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
// The function that solves the problem using backtracking
public static boolean solveNQueen(int board[][], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
//if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//backtrack if the above condition is false
board[i][col] = 0;
}
}
return false;
}
public static void main(String args[])
{
int board[][] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (!solveNQueen(board, 0)) {
System.out.print("Solution does not exist");
return;
}
printSolution(board);
}
}
Output :
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0

Nが8の場合、出力は以下の通りです。
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
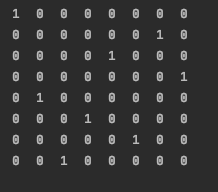
コードの実装を理解する
攻撃の対象であるかどうかを確認するために、私たちはisSafeという関数を作成しました。
その関数は、いかなる攻撃からも安全な位置であれば、trueを返します。
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
最初のforループは列をチェックします。2番目と3番目のforループは2つの対角線をチェックします。
次のコードは、クイーンを配置してバックトラックする責任を持ちます。クイーンの位置をマークするために、そのセルを行列内の1として設定します。クイーンを配置する前に、位置が安全であることを確認するためにisSafeを呼び出します。
public static boolean solveNQueen(int board[][], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
//if it is safe to place the queen at position i,col -> place it
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//backtrack if the above condition is false
board[i][col] = 0;
}
}
return false;
}
再帰呼び出しはボードを渡し、カラムを col+1 に設定します。再帰呼び出しが false を返した場合、エントリを0にリセットしてバックトラックします。
結論
バックトラッキングを使用してN-Queenの問題を解く方法は次のとおりです。バックトラッキングについてもっと学ぶためには、数独の問題を解くことを試してみてください。

