Pythonでの論理ゲート – 初心者にもわかりやすいガイド
この記事は、Pythonでのさまざまな論理ゲートを包括的に解説しています。論理ゲートは、デジタルコンポーネントを実装するために最も基本的な素材です。論理ゲートの使用は、コンピューターアーキテクチャから電子工学の領域まで広範です。
これらのゲートは、0または1のバイナリ値を扱います。異なる種類のゲートは異なる数の入力を受け取りますが、どれも単一の出力を提供します。これらの論理ゲートは組み合わせると複雑な回路を形成します。
Python言語で論理ゲートを実装してみましょう。 (Pythonげんごでろんりゲートをじっそうしてみましょう。)
Pythonにおける基本的な論理ゲート
回路開発には、3つの最も基本的な論理ゲートがあります。
ORゲート
このゲートは、入力のどちらかが1の場合、出力が1となります。バイナリ数に関しては、”加算”の操作に似ています。
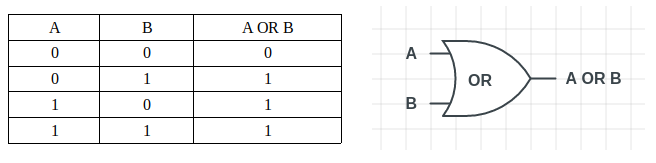
上に表示されているのは真理値表です。これは「OR」ゲートの入力のすべての値の組み合わせを示すために使用されます。表の横に描かれている図は「OR」ゲートを示しています。
Pythonによる実装方法:
# Function to simulate OR Gate
def OR(A, B):
return A | B
print("Output of 0 OR 0 is", OR(0, 0))
print("Output of 0 OR 1 is", OR(0, 1))
print("Output of 1 OR 0 is", OR(1, 0))
print("Output of 1 OR 1 is", OR(1, 1))
私たちは次の出力を得ます。 (Watashitachi wa tsugi no shutsuryoku o emasu.)
Output of 0 OR 0 is 0
Output of 0 OR 1 is 1
Output of 1 OR 0 is 1
Output of 1 OR 1 is 1
ANDゲート
このゲートは、入力のどちらかが0の場合、出力として0を提供します。この操作は、バイナリ数における掛け算と考えられています。
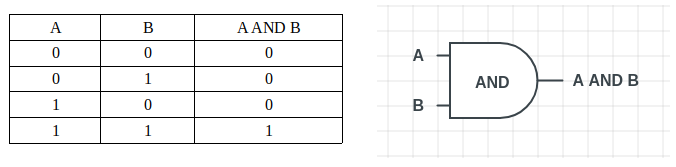
真理値表を見ると、2つの入力のどちらかが0の場合、出力も0であることがわかります。添付図は「AND」ゲートを示しています。
Pythonによる実装
# Function to simulate AND Gate
def AND(A, B):
return A & B
print("Output of 0 AND 0 is", AND(0, 0))
print("Output of 0 AND 1 is", AND(0, 1))
print("Output of 1 AND 0 is", AND(1, 0))
print("Output of 1 AND 1 is", AND(1, 1))
結果: 日本語でパラフレーズされたバージョンが必要です。
Output of 0 AND 0 is 0
Output of 0 AND 1 is 0
Output of 1 AND 0 is 0
Output of 1 AND 1 is 1
NOTゲート
このゲートは入力されたものの否定を提供します。このゲートは単一の入力のみサポートしています。

上記の表はビットの反転を明確に示しています。隣接する図は「NOT」ゲートを表しています。
バイナリNOTゲートのPython実装:
# Function to simulate NOT Gate
def NOT(A):
return ~A+2
print("Output of NOT 0 is", NOT(0))
print("Output of NOT 1 is", NOT(1))
出力:
出力結果:
Output of NOT 0 is 1
Output of NOT 1 is 0
注意:「NOT()」関数は、ビット値0と1に対して正しい結果を提供します。
Pythonにおけるユニバーサルロジックゲート
「NAND」と「NOR」という2つの普遍論理ゲートがあります。これらは普遍と呼ばれるのは、どんなブール回路もこれらのゲートだけを使って実装することができるからです。
NANDゲート
「NAND(ナンド)」ゲートは、「AND(アンド)」ゲートに続いて「NOT(ノット)」ゲートが組み合わさったものです。”AND”ゲートとは逆に、両方のビットがセットされている場合にのみ出力が0となり、それ以外では1を出力します。
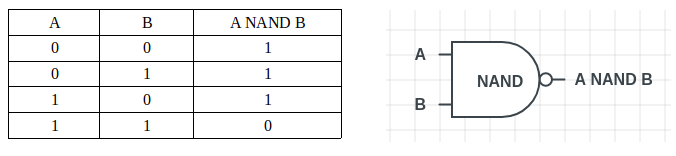
Pythonで、’NAND()’関数は、以前に作成した’AND()’と’OR()’関数を使用して実装することができます。
# Function to simulate AND Gate
def AND(A, B):
return A & B;
# Function to simulate NOT Gate
def NOT(A):
return ~A+2
# Function to simulate NAND Gate
def NAND(A, B):
return NOT(AND(A, B))
print("Output of 0 NAND 0 is", NAND(0, 0))
print("Output of 0 NAND 1 is", NAND(0, 1))
print("Output of 1 NAND 0 is", NAND(1, 0))
print("Output of 1 NAND 1 is", NAND(1, 1))
私たちは次の出力を得る
Output of 0 NAND 0 is 1
Output of 0 NAND 1 is 1
Output of 1 NAND 0 is 1
Output of 1 NAND 1 is 0
NORゲート
「NOR」ゲートは、「OR」ゲートに「NOT」ゲートを連結させた結果です。『OR』ゲートとは異なり、すべての入力が0の場合に出力1を提供します。
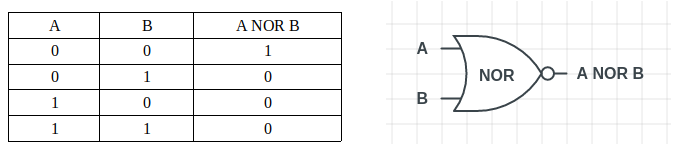
‘NAND()’関数に似たように、’NOR()’関数も既に作成された関数を使用して実装することができます。
# Function to calculate OR Gate
def OR(A, B):
return A | B;
# Function to simulate NOT Gate
def NOT(A):
return ~A+2
# Function to simulate NOR Gate
def NOR(A, B):
return NOT(OR(A, B))
print("Output of 0 NOR 0 is", NOR(0, 0))
print("Output of 0 NOR 1 is", NOR(0, 1))
print("Output of 1 NOR 0 is", NOR(1, 0))
print("Output of 1 NOR 1 is", NOR(1, 1))
出力:
Output of 0 NOR 0 is 1
Output of 0 NOR 1 is 0
Output of 1 NOR 0 is 0
Output of 1 NOR 1 is 0
Pythonにある排他的な論理ゲート
日本語での一つのオプションで以下の文を言い換えると、「XOR」と「XNOR」という特別な二つの論理ゲートがあり、個々の値ではなく、0または1の入力の数に焦点を当てています。
排他的論理和ゲート
エクスクルーシブ-オア(排他的論理和)の略称である「XOR」ゲートは、入力における1の数が奇数の場合に、出力が1となります。
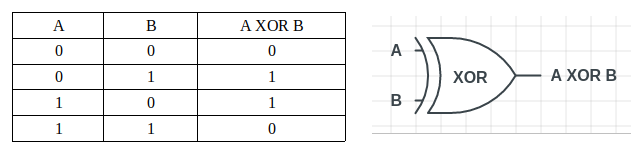
上の表から、XORゲートの出力が明確にわかります。入力中の1の個数が1つ、つまり奇数の場合には出力は1を提供しています。
Pythonで ‘XOR()’関数を簡単に実装することができます。
# Function to simulate XOR Gate
def XOR(A, B):
return A ^ B
print("Output of 0 XOR 0 is", XOR(0, 0))
print("Output of 0 XOR 1 is", XOR(0, 1))
print("Output of 1 XOR 0 is", XOR(1, 0))
print("Output of 1 XOR 1 is", XOR(1, 1))
私たちは次の出力を取得します。 (Watashitachi wa tsugi no shutsuryoku o shutoku shimasu.)
Output of 0 XOR 0 is 0
Output of 0 XOR 1 is 1
Output of 1 XOR 0 is 1
Output of 1 XOR 1 is 0
XNORゲート
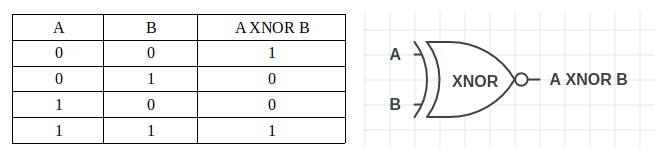
それは「XOR」と「NOT」ゲートの組み合わせによって形成されます。 「XOR」とは対照的に、入力の中の1の数が偶数の場合に、出力が1を提供します。
「XNOR()」関数は、Pythonで「XOR()」関数と「NOT()」関数を使って実装することができます。
# Function to simulate XOR Gate
def XOR(A, B):
return A ^ B
# Function to simulate NOT Gate
def NOT(A):
return ~A+2
# Function to simulate XNOR Gate
def XNOR(A, B):
return NOT(XOR(A, B))
print("Output of 0 XNOR 0 is", XNOR(0, 0))
print("Output of 0 XNOR 1 is", XNOR(0, 1))
print("Output of 1 XNOR 0 is", XNOR(1, 0))
print("Output of 1 XNOR 1 is", XNOR(1, 1))
出力:
Output of 0 XNOR 0 is 1
Output of 0 XNOR 1 is 0
Output of 1 XNOR 0 is 0
Output of 1 XNOR 1 is 1
結論
Pythonでの論理ゲートの実装は非常に簡単です。プログラマとして、Pythonの論理ゲートと演算子について知っている必要があります。本記事が読者にPythonでの論理ゲートの基礎と実行方法について理解を深めるお手伝いができればと願っています。
詳しくは、私たちの他のPythonチュートリアルを参照してください。

