「ハノイの塔」- アルゴリズムとJavaにおける実装
ハノイの塔は、プログラミングの世界で古典的な問題です。問題の設定には3本の棒またはピンとn枚のディスクがあります。
ディスクは一つの台から別の台に移動することができます。n枚のディスクは、サイズが異なります。
最初、すべてのディスクは最初の塔に積まれています。ディスクは常に自身より大きなディスクの上に積まれるようにしています。
ハノイの塔のデフォルトセットアップ
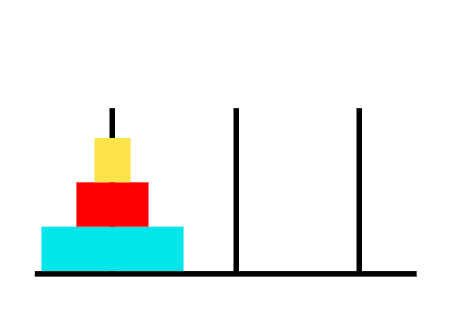
面白い事実: このゲームは19世紀にフランスの数学者エドゥアール・リュカによって発明されました。これは、パズルが若い僧侶の精神訓練に使用されたと言われるヒンドゥー寺院の伝説と関連しています。
問題の説明
Move all the disks stacked on the first tower over to the last tower using a helper tower in the middle. While moving the disks, certain rules must be followed. These are :
1. Only one disk can be moved.
2. A larger disk can not be placed on a smaller disk.
最初のタワーからすべてのディスクを最後のタワーへ移動する必要があります。一度に1つのディスクしか移動できず、小さなディスクの上に大きなディスクを置くことはできません。
これを行うためには、さらにヘルパー/補助タワーと呼ばれるタワーが必要です。
一度に1枚のディスクしか移動できないため、移動するディスクはそのタワーの一番上にある必要があります。
「ハノイの塔問題に対する理論的な解決策」
「A、B、C」とタワーを、そして「1、2、3」とディスクを名付けましょう。
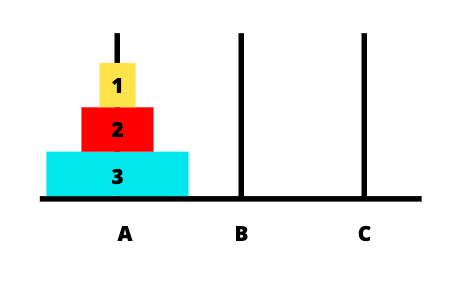
この問題は、単純な再帰を使って解決します。最終的な塔に3つのディスクを移動するには、次のようにする必要があります。
-
- ディスクの番号1と2をタワーBに持って行ってください。
-
- ディスクの番号3をタワーCに移動してください。
- ディスクの番号1と2をBからCに持って行ってください。
もちろん、制約のためにこのようにはできません。しかし、これを再帰的に行う機能を作成することができます。
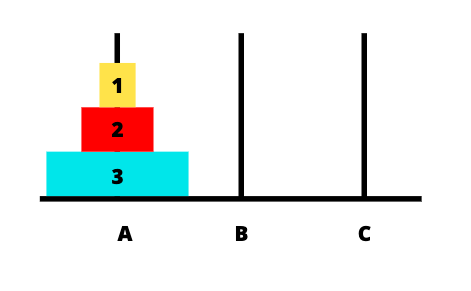
私たちが書く関数では、ディスクの移動をプリントします。
JavaでTower of Hanoiの解決策を実装する
「では、ハノイの塔問題を解くためのコードの主要な2つの部分を理解してみましょう。」
1. ベースケース
私たちのコードのベースケースは、ディスクが1つだけの場合です。つまり、 n=1です。
if (n == 1)
{
System.out.println("Take disk 1 from rod " + from_rod + " to rod " + to_rod);
return;
}
2. 再帰呼び出し
「ハノイの塔を解くための再帰呼び出しは次のようになります。」
towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
System.out.println("Take disk " + n + " from rod " + from_rod + " to rod " + to_rod);
towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
}
これらは以下と同等です。
-
- 上からn-1枚のディスクを補助のタワーに移動させる。
-
- ソースロッドからデスティネーションロッドに1枚のディスクを移動させる。
- 補助ディスクからn-1枚のディスクをデスティネーションロッドに移動させる。
タワーオブハノイの完全なJava実装
package com.JournalDev;
public class Main {
static void towerOfHanoi(int n, char from_rod, char to_rod, char helper_rod)
{
if (n == 1)
{
System.out.println("Take disk 1 from rod " + from_rod + " to rod " + to_rod);
return;
}
towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
System.out.println("Take disk " + n + " from rod " + from_rod + " to rod " + to_rod);
towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
}
public static void main(String args[])
{
int n = 5;
towerOfHanoi(n,'A','C', 'B');
}
}
コードの出力は次の通りです:
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
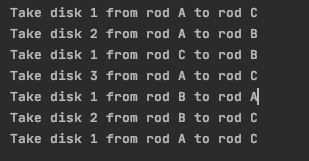
下の図を使ってプロセスを理解することができます。任意の数のディスクでコードを実行することができます。
n = 5 の 出力は :
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 4 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 2 from rod C to rod A
Take disk 1 from rod B to rod A
Take disk 3 from rod C to rod B
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 5 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 3 from rod B to rod A
Take disk 1 from rod C to rod B
Take disk 2 from rod C to rod A
Take disk 1 from rod B to rod A
Take disk 4 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
n枚のディスクのステップの数を計算するための公式は次の通りです。
(2^n)-1
結論
再帰を使ってハノイの塔を解く方法をご紹介します。一緒に学んで楽しんでいただけたと嬉しいです!

