在Python中的K-近邻算法（KNN）

k-最近邻算法（kNN）是一种监督式机器学习技术，可用于处理分类和回归任务。我认为KNN是一种源自实际生活的算法。人们往往会受到周围人的影响。

K-最近邻算法背后的思想

我们的行为是由我们一起长大的伙伴所塑造的。我们的父母也以各种方式塑造了我们的个性。如果你在喜欢运动的人群中长大，很可能你会喜欢上运动。当然也有例外情况。KNN的工作原理类似。

如果你有一个亲密的朋友，并且大部分时间都和他/她在一起，最终你们会拥有相似的兴趣爱好和喜爱相同的事物。这就是kNN算法，其中k=1。
如果你经常和一个由5个人组成的团体一起玩耍，团体中的每个人对你的行为都有影响，最终你会变成这五个人的平均值。这就是kNN算法，其中k=5。

kNN分类器使用多数投票原则来确定数据点的类别。如果k设定为5，将会考察5个最近点的类别。根据占优势的类别进行预测。类似地，kNN回归会使用5个最近位置的平均值。

我们是否目击过那些看似亲近的人，但数据点之间如何被认为是亲近的？数据点之间的距离是被测量的。有各种技术来估算距离。欧氏距离（当p=2时的闵可夫斯基距离）是最常用的距离测量之一。下图解释了如何计算在二维空间中两点之间的欧氏距离。它是通过位置的x和y坐标差的平方来确定的。

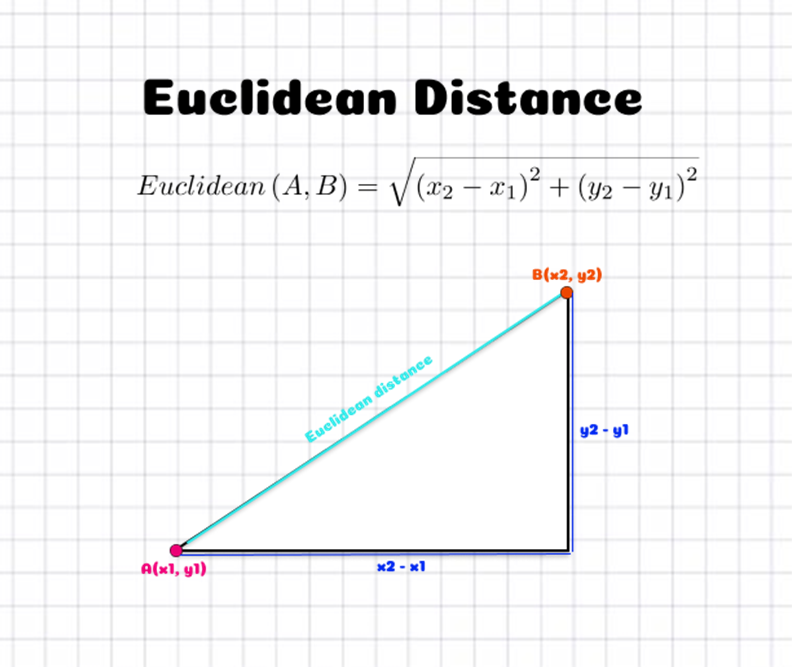
在Python中实现KNN算法

现在让我们来实际进行Python中的KNN实现。我们将详细介绍步骤，帮助您分解代码并更好地理解它。

导入模块

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

2. 创建数据集

Scikit-learn拥有许多用于创建合成数据集的工具，非常适用于测试机器学习算法。我将使用make blobs方法进行操作。

X, y = make_blobs(n_samples = 500, n_features = 2, centers = 4,cluster_std = 1.5, random_state = 4)

这段代码会生成一个包含500个样本的数据集，分为四个类别，总共有两个特征。使用关联的参数，您可以快速更改样本数量、特征和类别。我们还可以更改每个聚类（或类别）的分布。

3. 数据集可视化

plt.style.use('seaborn')
plt.figure(figsize = (10,10))
plt.scatter(X[:,0], X[:,1], c=y, marker= '*',s=100,edgecolors='black')
plt.show()

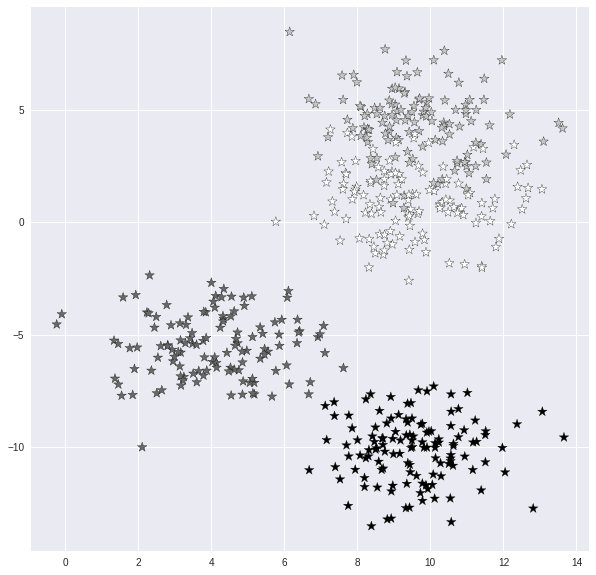
将数据分成训练集和测试集。

对于每个监督式机器学习方法来说，将数据集划分为训练集和测试集非常重要。我们首先训练模型，然后在数据集的不同部分进行测试。如果我们不对数据进行分离，实际上是在使用模型已经了解的数据进行测试。使用train_test_split方法，我们可以简单地将测试分离出来。

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)

通过训练集大小和测试集大小选项，我们可以确定原始数据中分别用于训练和测试集的比例。默认情况下，训练集占总数据的75%，测试集占25%。

5. KNN分类器的实现

然后，我们将构建一个kNN分类器对象。我使用k值为1和5开发了两个分类器，以展示k值的相关性。然后使用训练集对这些模型进行训练。选择k值是使用n_neighbors参数完成的。因为默认值为5，所以不需要显式地指定。

knn5 = KNeighborsClassifier(n_neighbors = 5)
knn1 = KNeighborsClassifier(n_neighbors=1)

6. KNN分类器的预测

然后，在测试集中，我们预测目标值并将其与实际值进行比较。

knn5.fit(X_train, y_train)
knn1.fit(X_train, y_train)

y_pred_5 = knn5.predict(X_test)
y_pred_1 = knn1.predict(X_test)

7. 预测k值的准确度

from sklearn.metrics import accuracy_score
print("Accuracy with k=5", accuracy_score(y_test, y_pred_5)*100)
print("Accuracy with k=1", accuracy_score(y_test, y_pred_1)*100)

k的值的准确性如下所示：

Accuracy with k=5 93.60000000000001
Accuracy with k=1 90.4

8. 预测可视化

让我们以 k=5 和 k=1 的值来观察测试集和预测值，看看 k 值的影响。

plt.figure(figsize = (15,5))
plt.subplot(1,2,1)
plt.scatter(X_test[:,0], X_test[:,1], c=y_pred_5, marker= '*', s=100,edgecolors='black')
plt.title("Predicted values with k=5", fontsize=20)

plt.subplot(1,2,2)
plt.scatter(X_test[:,0], X_test[:,1], c=y_pred_1, marker= '*', s=100,edgecolors='black')
plt.title("Predicted values with k=1", fontsize=20)
plt.show()

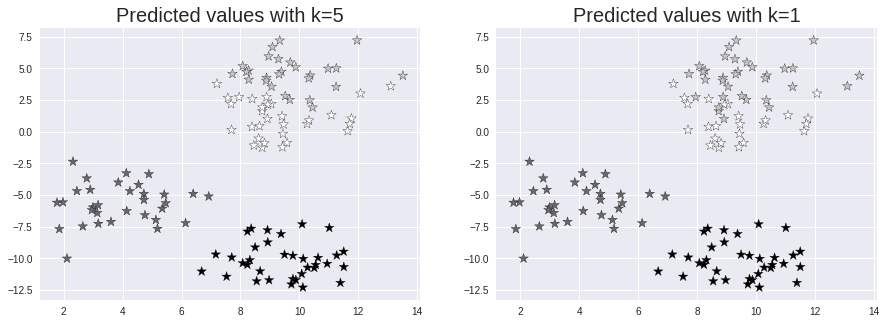
如何找到最佳的k值来实现KNN算法

k=1：模型过于狭窄且泛化能力不足，对噪声非常敏感。该模型在训练集上对新的、以前未知的数据点进行高度准确的预测，但在全新的、以前未见的数据点上却是一个较差的预测器。因此，我们很可能得到一个过拟合的模型。
k=100：该模型过于宽泛，在训练集和测试集上都不可靠。此种情况被称为欠拟合。

KNN算法的限制

KNN是一个简单易懂的算法。它不依赖于任何内部机器学习模型来生成预测。KNN是一种分类方法，只需知道有多少个类别就可以工作（一个或多个）。这意味着它可以快速评估是否应该添加一个新的类别，而无需知道其他类别的数量。

这种简单性的缺点是它无法预测异常情况（如新疾病），这是KNN无法完成的，因为它不知道在健康人群中罕见项目的普遍程度。

尽管KNN在测试集上能够达到较高的准确度，但在时间和内存方面它较慢且更昂贵。为了进行预测，它需要相当大的内存来存储整个训练数据集。此外，由于欧几里得距离对数据的大小具有很高的敏感性，具有大数值特征的数据将始终比具有小数值特征的数据更为重要。

最后，在考虑到我们所讨论的一切之后，我们应该记住KNN并不适用于大维度的数据集。

结论

希望你现在对KNN算法有了更好的理解。我们已经探讨了多种关于KNN如何保存完整数据集以生成预测的思路。

KNN是几种惰性学习算法之一，它不使用学习模型进行预测。通过计算传入观测与已有数据之间的相似性的平均值，KNN实时生成预测。

谢谢你的阅读！