如何找到链表的长度?
链表是什么?
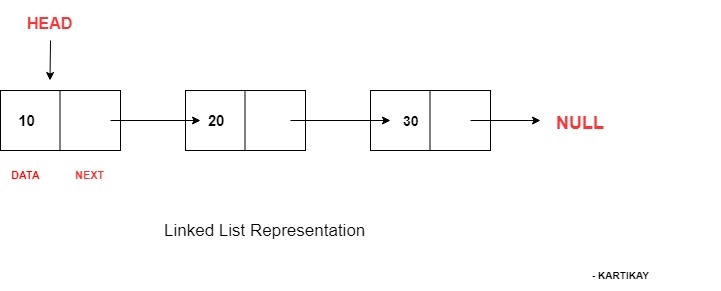
- A linked list is a linear data structure used for storing collections of data
- Successive elements are connected by pointers
- The last element points to NULL
- Each element is a separate object and is called a Node
- Each node in a linked list comprises of two partsData
Reference to Next Node
如何找到链表的长度?
找到链表的长度有两种方法。
-
- 迭代方法
- 递归方法
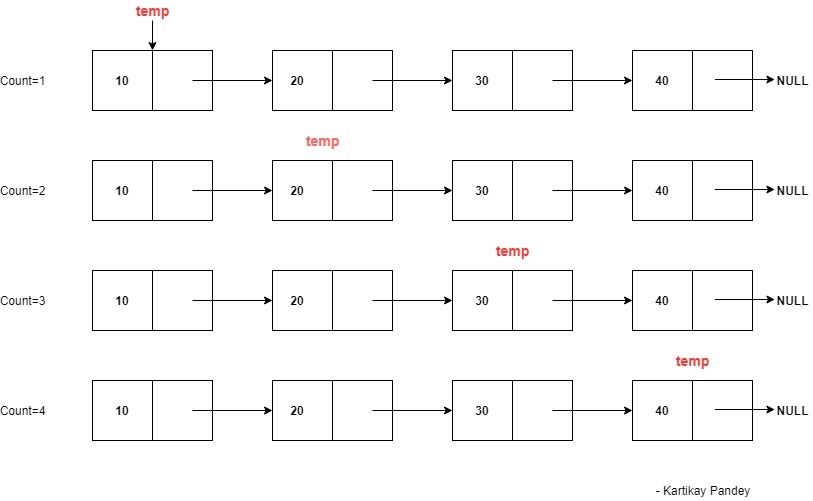
使用迭代方法计算链表的长度
我们将使用链表遍历来找到链表的长度。
- Head Points to the First Node of The List.
- Initialize the count variable with value 0
- Initialize the temp variable with Head
- As we access each Node, the value of count variable is increased by 1.
- Stop The process when we reach null.
- Do not change the head reference.
用Java编码
package com.Olivia.ds;
public class MyLinkedList {
public class Node {
int data;
Node next;
}
public Node head;
public Node tail;
public int size;
public int getFirst() throws Exception {
if (this.size == 0) {
throw new Exception("linked list is empty");
}
return this.head.data;
}
public int getLast() throws Exception {
if (this.size == 0) {
throw new Exception("linked list is empty");
}
return this.tail.data;
}
public void display() {
Node temp = this.head;
while (temp != null) {
System.out.println(temp.data + " ");
temp = temp.next;
}
}
public void addFirst(int item) {
Node nn = new Node();
nn.data = item;
if (this.size == 0) {
this.head = nn;
this.tail = nn;
this.size = this.size + 1;
} else {
nn.next = this.head;
this.head = nn;
this.size = this.size + 1;
}
}
public int length() {
Node temp = this.head;
int count = 0;
while (temp != null) {
count++;
temp = temp.next;
}
return count;
}
public static void main(String[] args) {
MyLinkedList ll = new MyLinkedList();
ll.addFirst(10);
ll.addFirst(20);
ll.addFirst(30);
ll.addFirst(40);
ll.addFirst(50);
System.out.println("Length of Linked List is " + ll.length());
}
}
在C语言中编码
#include <stdio.h>
#include <stdlib.h>
/* A structure of linked list node */
struct node {
int data;
struct node *next;
} *head;
void initialize(){
head = NULL;
}
/*
Inserts a node in front of a singly linked list.
*/
void insert(int num) {
/* Create a new Linked List node */
struct node* newNode = (struct node*) malloc(sizeof(struct node));
newNode->data = num;
/* Next pointer of new node will point to head node of linked list */
newNode->next = head;
/* make new node as the new head of linked list */
head = newNode;
printf("Inserted Element : %d\n", num);
}
int getLength(struct node *head){
int length =0;
while(head != NULL){
head = head->next;
length++;
}
return length;
}
/*
Prints a linked list from head node till the tail node
*/
void printLinkedList(struct node *nodePtr) {
while (nodePtr != NULL) {
printf("%d", nodePtr->data);
nodePtr = nodePtr->next;
if(nodePtr != NULL)
printf("-->");
}
}
int main() {
initialize();
/* Creating a linked List*/
insert(8);
insert(3);
insert(2);
insert(7);
insert(9);
printf("\nLinked List\n");
printLinkedList(head);
printf("\nLinked List Length : %d", getLength(head));
return 0;
}
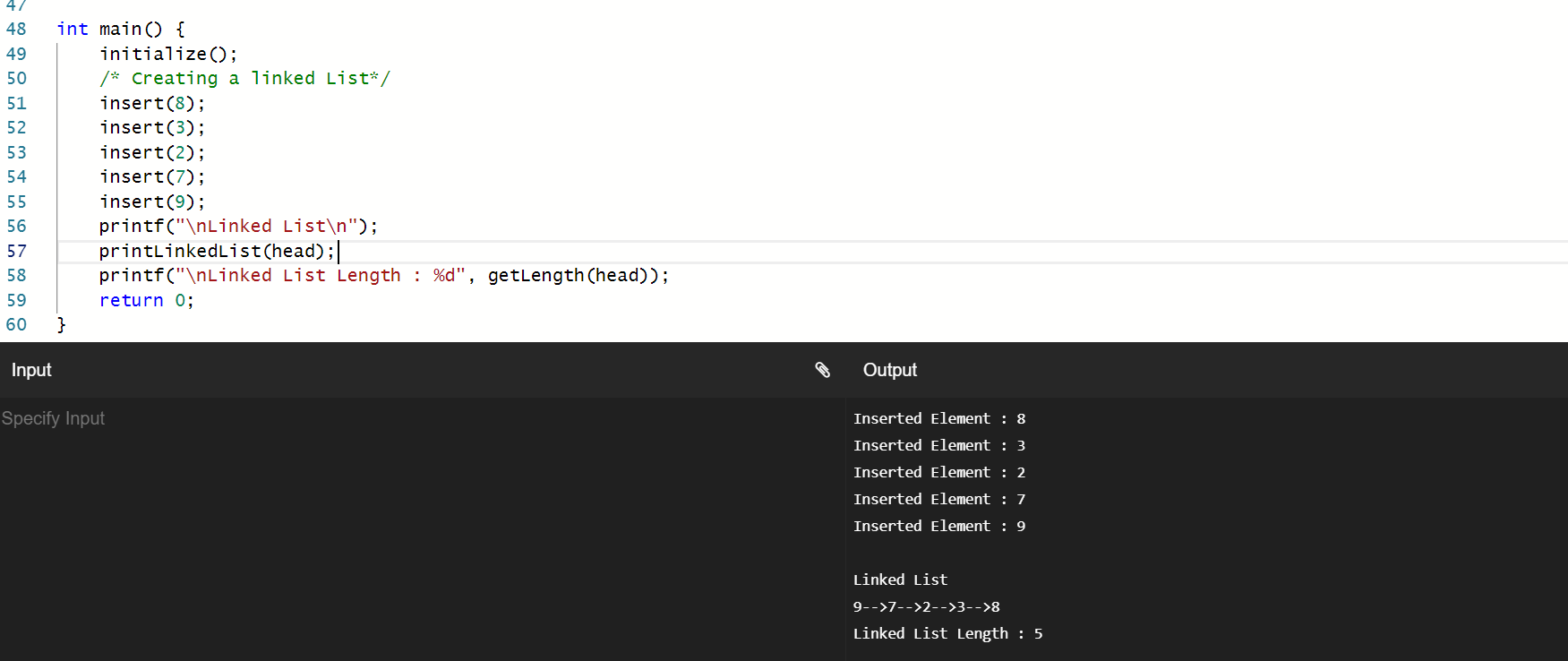
结果
使用递归解决方案计算链表的长度。
基础情况:
- Last Node points to Null value
- Return 0
递归情况:
- At each step update the Value of Current Node to the Next Node
- Call= 1+fun(curr.next)
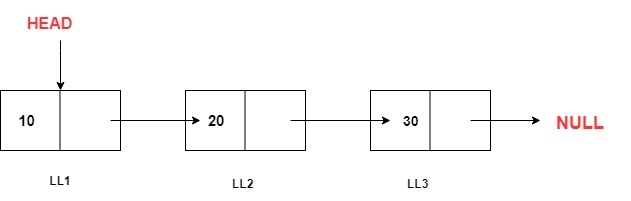
在链表中有3个元素:LL1、LL2和LL3。当进行递归调用时,我们将观察内存堆栈中发生的情况。内存堆栈:
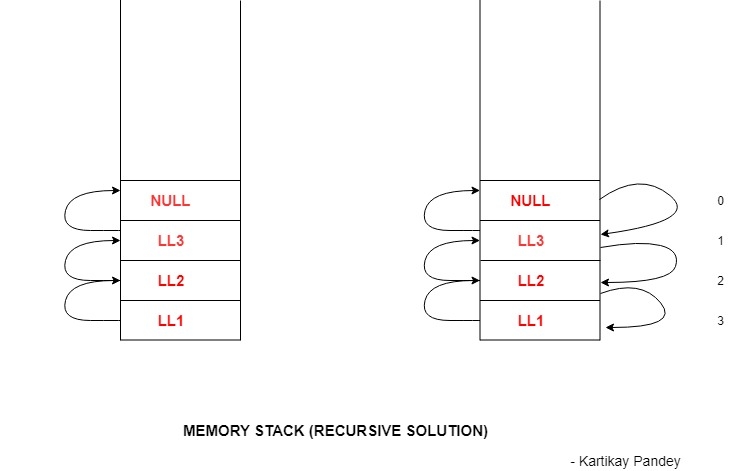
主函数调用LL1,LL1调用LL2,LL2调用LL3,LL3调用空值。
当达到空值时,我们从这里返回。0被返回给LL3,LL3向LL2返回1,LL2向LL1返回2,最后LL1向主函数返回3。
使用Java进行编码
package com.Olivia.ds;
public class MyLinkedList {
public class Node {
int data;
Node next;
}
public Node head;
public Node tail;
public int size;
public int getfirst() throws Exception {
if (this.size == 0) {
throw new Exception("linked list is empty");
}
return this.head.data;
}
public int RemoveFirst() throws Exception {
if (this.size == 0) {
throw new Exception("LL is empty");
}
Node temp = this.head;
if (this.size == 1) {
this.head = null;
this.tail = null;
size = 0;
} else {
this.head = this.head.next;
this.size--;
}
return temp.data;
}
public void addFirst(int item) {
Node nn = new Node();
nn.data = item;
if (this.size == 0) {
this.head = nn;
this.tail = nn;
this.size = this.size + 1;
} else {
nn.next = this.head;
this.head = nn;
this.size = this.size + 1;
}
}
public int lengthUsingRecursiveApproach (){
return lengthUsingRecursiveApproach(this.head);
}
private int lengthUsingRecursiveApproach(Node curr) {
// TODO Auto-generated method stub
if (curr == null) {
return 0;
}
return 1 + lengthUsingRecursiveApproach (curr.next);
}
public static void main(String[] args) {
MyLinkedList ll = new MyLinkedList();
// insert elements into the Linked List
ll.addFirst(10);
ll.addFirst(20);
ll.addFirst(30);
ll.addFirst(40);
ll.addFirst(50);
// Length of List
System.out.println("Recursive Approach length " + ll.lengthUsingRecursiveApproach(ll.head));
}
}
在C语言中编写代码。
#include <stdio.h>
struct Node
{
int data;
struct Node* next;
};
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
/* link the old list of the new node */
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int getCount(struct Node* head)
{
// Base case
if (head == NULL)
return 0;
return 1 + getCount(head->next);
}
int main()
{
struct Node* head = NULL;
push(&head, 1);
push(&head, 3);
push(&head, 1);
push(&head, 2);
push(&head, 1);
printf("count of nodes is %d", getCount(head));
return 0;
}
输出
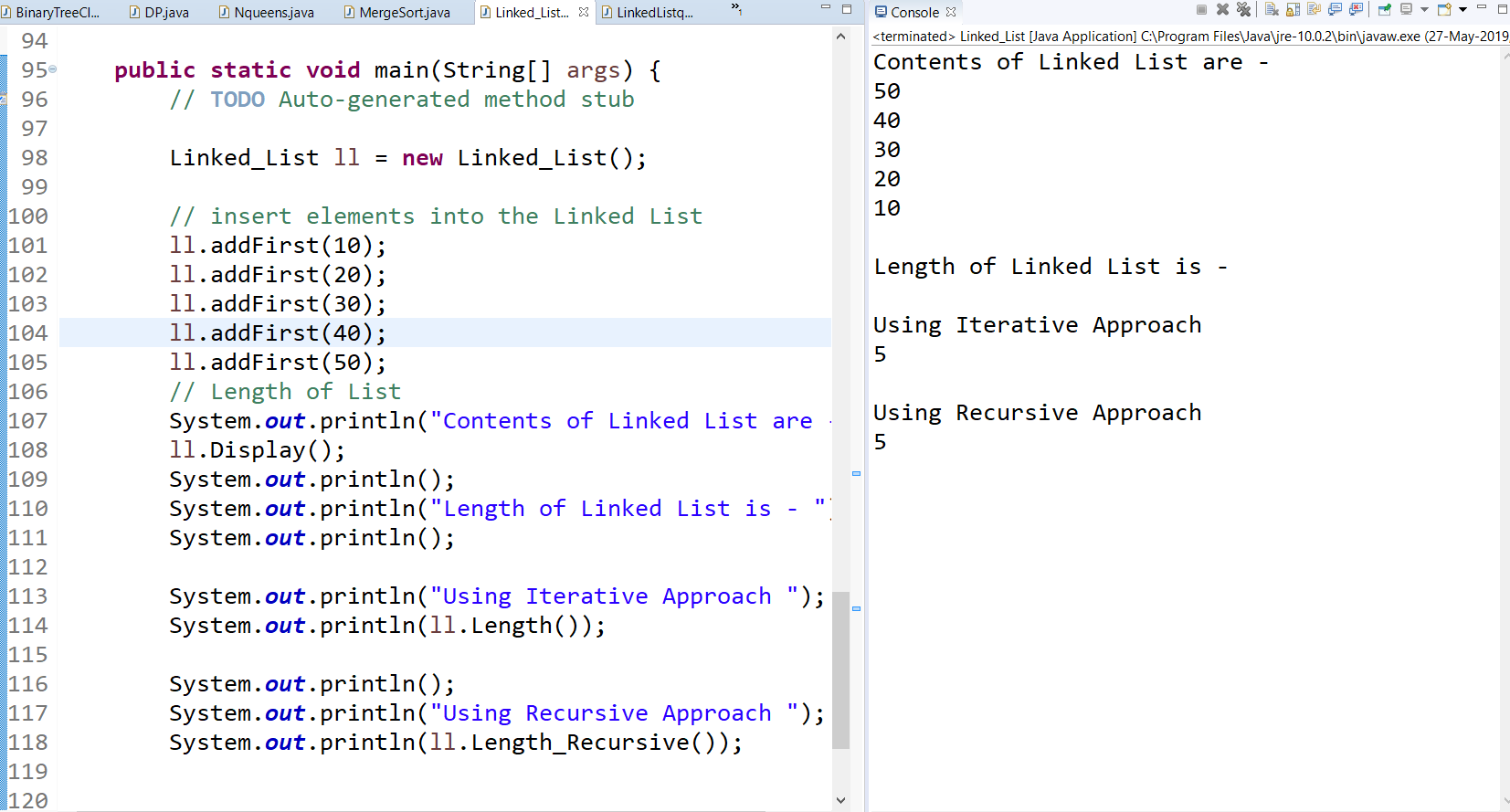
时间复杂度
在递归和迭代解决方案中,时间复杂度均为O(N),因为我们只需要进行一次遍历来得知长度。

