汉诺塔 – Java 中的算法和实现

12 月 ago

科, 颖

3 minutes

汉诺塔是编程世界中的经典问题。问题的设置包括三根杆子/桩和n个盘子。

可以将盘子从一个针上移动到另一个针上。这 n 个盘子的大小都不同。

最初所有的圆盘都叠在第一座塔上，圆盘的叠放方式是始终要放在比自己大的圆盘之上。

汉诺塔的默认设置

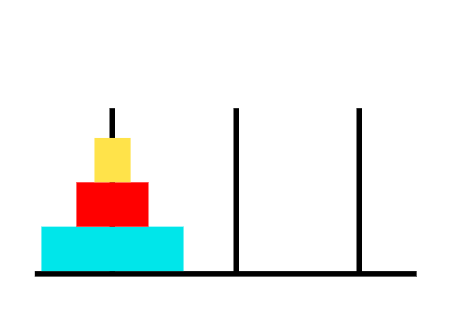
有趣的事实：这个游戏是由19世纪的法国数学家埃德华·卢卡斯发明的。它与一座印度教寺庙的传说相关，据称这个谜题被用来增强年轻僧侣的心理纪律能力。

问题陈述

Move all the disks stacked on the first tower over to the last tower using a helper tower in the middle. While moving the disks, certain rules must be followed. These are : 

1. Only one disk can be moved.

2. A larger disk can not be placed on a smaller disk.

所以你需要把所有的盘子从第一座塔移动到最后一座塔上。你每次只能移动一个盘子，并且不能把较小的盘子放在较大的盘子上。

为了做到这一点，您需要额外的塔楼，它被称为辅助塔楼。

由于每次只能移动一个盘子，所以你移动的盘子必须位于其所在塔的顶部。

汉诺塔问题的理论解决方案

让我们把塔命名为A、B、C，将圆盘称为1、2、3。

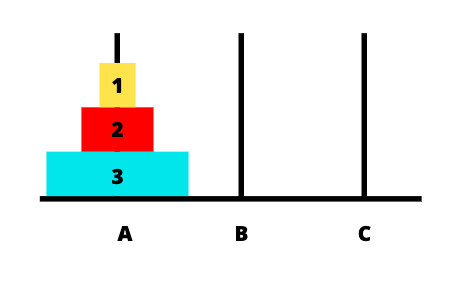
我们使用简单的递归来解决这个问题。要将这三个盘子移到最后一个塔上，你需要：

将1号和2号碟子从B塔移到C塔。

当然，由于限制，在这种方式下你不能这样做。然而，我们可以利用这个来创建一个可以递归执行的函数。

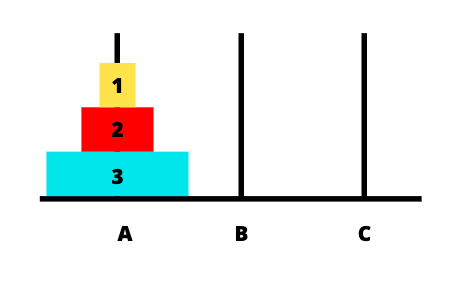
在我们编写的函数中，我们将打印出盘子的移动。

用Java实现汉诺塔问题的解决方案

让我们从了解解决汉诺塔问题所需的代码的两个主要部分开始。

基本情况

我们代码中的基本情况是当我们只有一个磁盘时，即n=1。

 if (n == 1)
        {
            System.out.println("Take disk 1 from rod " +  from_rod + " to rod " + to_rod);
            return;
        }

2. 递归调用

汉诺塔问题的递归调用如下：

 towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
        System.out.println("Take disk " + n + " from rod " +  from_rod + " to rod " + to_rod);
        towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
    }

这些与以下相等：

将辅助杆上的n-1个盘子移到目标杆上。

《汉诺塔游戏》的完整Java实现

package com.JournalDev;
public class Main {
    static void towerOfHanoi(int n, char from_rod, char to_rod, char helper_rod)
    {
        if (n == 1)
        {
            System.out.println("Take disk 1 from rod " +  from_rod + " to rod " + to_rod);
            return;
        }
        towerOfHanoi(n-1, from_rod, helper_rod, to_rod);
        System.out.println("Take disk " + n + " from rod " +  from_rod + " to rod " + to_rod);
        towerOfHanoi(n-1, helper_rod, to_rod, from_rod);
    }

    public static void main(String args[])
    {
        int n = 5;
        towerOfHanoi(n,'A','C', 'B');
    }

}

代码的输出为：

Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C

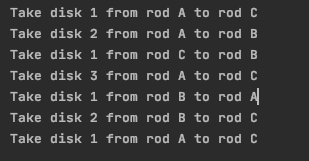
我们可以通过以下插图来理解这个过程。您可以运行代码来设置任意数量的盘子。

当n=5时，输出结果为:

Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 4 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 2 from rod C to rod A
Take disk 1 from rod B to rod A
Take disk 3 from rod C to rod B
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 5 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 3 from rod B to rod A
Take disk 1 from rod C to rod B
Take disk 2 from rod C to rod A
Take disk 1 from rod B to rod A
Take disk 4 from rod B to rod C
Take disk 1 from rod A to rod C
Take disk 2 from rod A to rod B
Take disk 1 from rod C to rod B
Take disk 3 from rod A to rod C
Take disk 1 from rod B to rod A
Take disk 2 from rod B to rod C
Take disk 1 from rod A to rod C

计算n个盘子的步数的公式为：

(2^n)-1

结论

这就是使用递归解决汉诺塔问题的方法。希望你在我们的学习中玩得开心！