Python实现逻辑门:从基础到应用,新手入门指南
本文全面介绍了如何在Python中实现不同的逻辑门。逻辑门是构建数字电路最基本的组成部分,其应用范围广泛,从计算机体系结构到各类电子设备都离不开它们。
这些逻辑门处理二进制值,即0或1。不同类型的逻辑门需要不同数量的输入,但它们都只产生一个单一的输出。当这些逻辑门巧妙地组合在一起时,就能形成复杂的数字电路。
接下来,让我们尝试使用Python语言来实现这些逻辑门。
Python中的基本逻辑门
在电路开发中,有三种最基本的逻辑门。
或门(OR Gate)
当“或门”的两个输入中任意一个为1时,其输出为1。这类似于二进制数的“加法”操作。
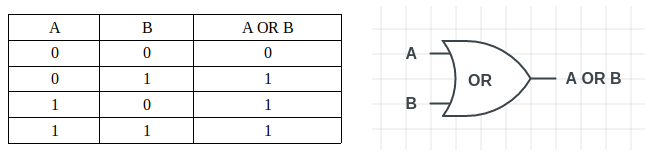
上方展示的是“或门”的真值表,它列出了所有可能的输入组合及其对应的输出。表格旁边的图示代表了“或门”的符号。
在Python中实现“或门”:
# 模拟或门功能的函数
def OR(A, B):
return A | B
print("0 或 0 的输出是", OR(0, 0))
print("0 或 1 的输出是", OR(0, 1))
print("1 或 0 的输出是", OR(1, 0))
print("1 或 1 的输出是", OR(1, 1))
运行上述代码,我们将得到如下输出:
0 或 0 的输出是 0
0 或 1 的输出是 1
1 或 0 的输出是 1
1 或 1 的输出是 1
与门(AND Gate)
“与门”的输出为0,只要其输入中有一个为0。在二进制运算中,这类似于“乘法”操作。
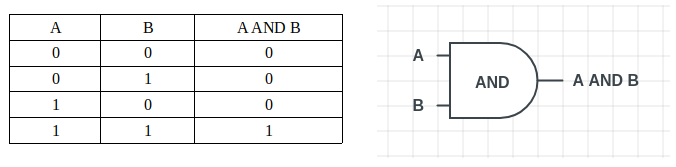
从真值表中可以看出,只要“与门”的两个输入中任意一个为0,其输出也为0。旁边的图示代表了“与门”的符号。
在Python中实现“与门”:
这是文章《Python中的逻辑门 – 一份适合初学者的指南》的第2部分(共6部分)。
# 模拟与门(AND Gate)的函数
def AND(A, B):
return A & B
print("0 与 0 的输出是", AND(0, 0))
print("0 与 1 的输出是", AND(0, 1))
print("1 与 0 的输出是", AND(1, 0))
print("1 与 1 的输出是", AND(1, 1))
输出:
0 与 0 的输出是 0
0 与 1 的输出是 0
1 与 0 的输出是 0
1 与 1 的输出是 1
非门(NOT Gate)
非门提供输入的逻辑反转。此门只支持一个输入。

上述表格清楚地显示了位的反转。相邻的图形代表了“非”门。
二进制非门的Python实现:
# 模拟非门(NOT Gate)的函数
def NOT(A):
return ~A+2
print("非 0 的输出是", NOT(0))
print("非 1 的输出是", NOT(1))
输出:
非 0 的输出是 1
非 1 的输出是 0
注意:’NOT()’函数对于位值0和1提供准确的结果。
Python中的通用逻辑门
存在两个通用逻辑门,即“与非门”(NAND Gate)和“或非门”(NOR Gate)。它们被称为通用逻辑门,因为任何布尔电路都可以仅使用这些门来实现。
与非门(NAND Gate)
“与非门”是由“与门”(AND Gate)和“非门”(NOT Gate)组合而成的。与“与门”相反,当两个输入位都为1时,它只输出0,否则输出1。
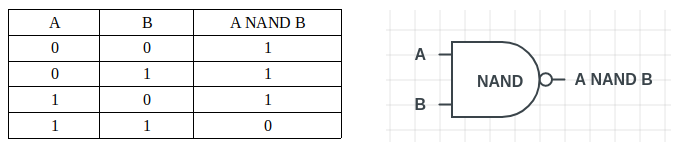
在Python中,可以使用之前创建的’AND()’和’NOT()’函数来实现’NAND()’函数。
# 模拟与门(AND Gate)的函数
def AND(A, B):
return A & B;
# 模拟非门(NOT Gate)的函数
def NOT(A):
return ~A+2
# 模拟与非门(NAND Gate)的函数
def NAND(A, B):
return NOT(AND(A, B))
print("0 NAND 0 的输出是", NAND(0, 0))
print("0 NAND 1 的输出是", NAND(0, 1))
print("1 NAND 0 的输出是", NAND(1, 0))
print("1 NAND 1 的输出是", NAND(1, 1))
我们得到了以下输出:
0 NAND 0 的输出是 1
0 NAND 1 的输出是 1
1 NAND 0 的输出是 1
1 NAND 1 的输出是 0
或非门 (NOR Gate)
“或非门”(NOR门)是通过级联“或门”(OR门)和“非门”(NOT门)得到的结果。与“或门”相反,当所有输入都为0时,它输出为1。
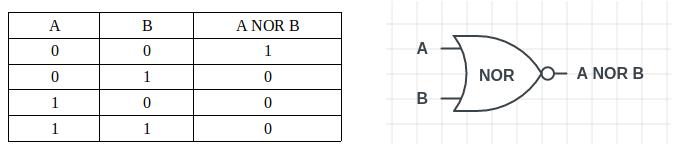
类似于“NAND()”函数,可以使用已经创建的函数来实现“NOR()”。
# 计算或门的函数
def OR(A, B):
return A | B;
# 模拟非门的函数
def NOT(A):
return ~A+2
# 模拟或非门的函数
def NOR(A, B):
return NOT(OR(A, B))
print("0 或非 0 的输出是", NOR(0, 0))
print("0 或非 1 的输出是", NOR(0, 1))
print("1 或非 0 的输出是", NOR(1, 0))
print("1 或非 1 的输出是", NOR(1, 1))
输出结果:
0 或非 0 的输出是 1
0 或非 1 的输出是 0
1 或非 0 的输出是 0
1 或非 1 的输出是 0
Python中的异或逻辑门
有两种特殊类型的逻辑门:异或门(XOR)和同或门(XNOR)。它们关注的是输入中“1”的数量是奇数还是偶数,而不是各个输入值。
异或门
异或门(’XOR’)是“Exclusive-OR”的缩写,当输入中“1”的数量为奇数时,它会输出“1”。
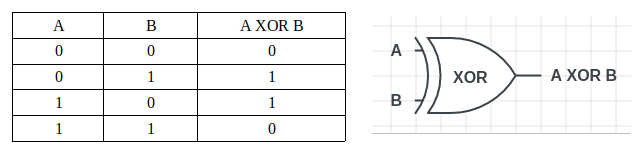
我们可以清楚地看到上表中异或门的输出。当输入中“1”的数量为1时(即奇数),它会输出“1”。
我们可以通过以下方式在Python中轻松实现’XOR()’函数:
# 模拟异或门(XOR Gate)的函数
def XOR(A, B):
return A ^ B
print("0 XOR 0 的输出是", XOR(0, 0))
print("0 XOR 1 的输出是", XOR(0, 1))
print("1 XOR 0 的输出是", XOR(1, 0))
print("1 XOR 1 的输出是", XOR(1, 1))
我们获得了如下的输出结果。
0 XOR 0 的输出是 0
0 XOR 1 的输出是 1
1 XOR 0 的输出是 1
1 XOR 1 的输出是 0
同或门(XNOR门)
同或门是由“异或门(XOR)”和“非门(NOT)”组合而成的。与“异或门”相反,当输入中“1”的数量为偶数时,同或门会输出“1”。
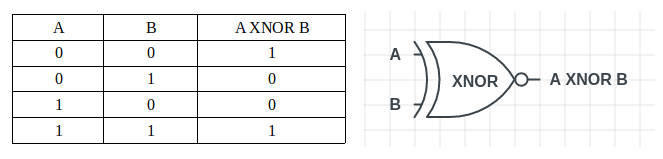
在Python中,可以通过结合使用“XOR()”函数和“NOT()”函数来实现“XNOR()”函数。
# 模拟异或门(XOR Gate)的函数
def XOR(A, B):
return A ^ B
# 模拟非门(NOT Gate)的函数
def NOT(A):
return ~A+2
# 模拟同或门(XNOR Gate)的函数
def XNOR(A, B):
return NOT(XOR(A, B))
print("0 XNOR 0 的输出是", XNOR(0, 0))
print("0 XNOR 1 的输出是", XNOR(0, 1))
print("1 XNOR 0 的输出是", XNOR(1, 0))
print("1 XNOR 1 的输出是", XNOR(1, 1))
输出:
0 XNOR 0 的输出是 1
0 XNOR 1 的输出是 0
1 XNOR 0 的输出是 0
1 XNOR 1 的输出是 1
结论
在 Python 中实现逻辑门非常简单。作为一名程序员,您需要了解 Python 中的逻辑门及其运算符。我们希望本文能让读者对 Python 中逻辑门的基础知识和实现方法有更清晰的认识。
如需进一步阅读,请查阅我们的其他 Python 教程。

