最小堆二叉树

一个最小堆二叉树是一棵二叉树，其中根节点的关键字是树中的最小值。

上述定义对树中的所有子树都适用，这被称为最小堆属性。

除了最后两层以外，几乎每个节点必须有两个子节点。也就是说，除了最后两层之外，这几乎是一棵完全二叉树。

以下树是一个最小堆二叉树的示例，因为上述两个属性成立。

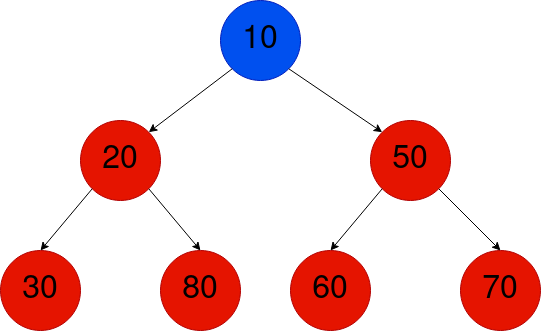
既然我们已经讲解了什么是小根堆树，那么现在让我们看看如何表示它。

---

Min Heap Tree的表示

一个最小堆二叉树通常用数组表示，数组的索引按以下格式排序。

整个树的根节点是 arr[0]。

我们将使用下图所示的索引。在这里找到匹配上表的模式并不太困难。

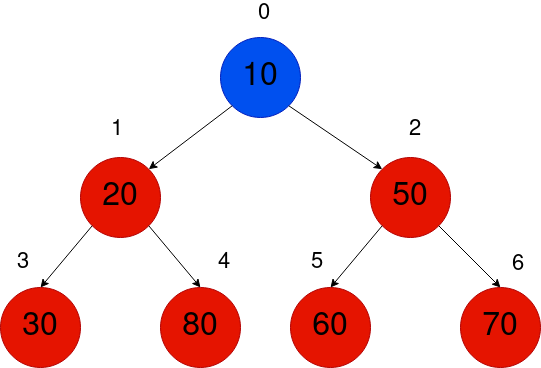
这种索引方式遵循二叉树的层序遍历，因此二叉堆数组是使用层序遍历的二叉树。

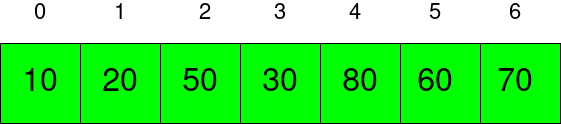
上图显示了最小堆树的数组表示。

现在我们已经了解了这些概念，让我们开始在C语言中实施吧！

---

实现一个小顶堆树

我们将使用数组表示来构建树。让我们开始编写最小堆的结构。

typedef struct MinHeap MinHeap;
struct MinHeap {
    int* arr;
    // Current Size of the Heap
    int size;
    // Maximum capacity of the heap
    int capacity;
};

我们会有一个元素数组和一个大小，大小会在插入或删除元素时进行更新。

数组还有一个容量，用来表示数组的最大尺寸。

我们需要写几个函数来表示我们正在表示一个最小堆，比如找到父节点和子节点。

int parent(int i) {
    // Get the index of the parent
    return (i - 1) / 2;
}

int left_child(int i) {
    return (2*i + 1);
}

int right_child(int i) {
    return (2*i + 2);
}

int get_min(MinHeap* heap) {
    // Return the root node element,
    // since that's the minimum, by the min-heap
    // property
    return heap->arr[0];
}

我们将编写函数来初始化和释放堆内存。

MinHeap* init_minheap(int capacity) {
    MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
    minheap->arr = (int*) calloc (capacity, sizeof(int));
    minheap->capacity = capacity;
    minheap->size = 0;
    return minheap;
}

void free_minheap(MinHeap* heap) {
    if (!heap)
        return;
    free(heap->arr);
    free(heap);
}

好的，既然这个问题解决了，现在让我们来讨论如何插入元素吧！

插入到小顶堆中

插入算法很简单。它将一个元素插入到树中。

分解算法:

• First, always insert at the bottom of the tree. The initial position of the inserted element is at the last level.
• We will now need to update the position of this element so that the min-heap property is satisfied.
• Since the root node of every sub-tree must be the minimum, check the sub-tree of its immediate parent.
• If the parent is greater than this inserted element, we need to update its position by swapping it.
• But we are not yet done, since the min-heap property may be violated of the updated node’s sub-tree!
• We need to keep swapping until we reach the root node, after which we are done.

为了理解这个过程，让我们举个例子来说明。

考虑下方仅含有一个元素的树。

让我们插入元素40。由于只有一个元素，它被插入到底部，并且我们观察到最小堆属性得到满足，因为10 < 40。所以不需要进行交换。

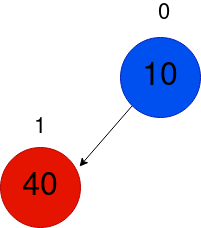
接下来，我们将插入50。随后进行类似的步骤。

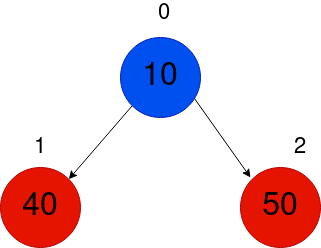
接下来，我们将插入5。现在，我们首先在树的底部插入，在索引3处。

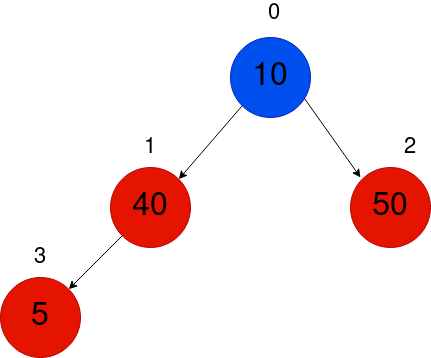
子树1-3违反了最小堆的属性，因此整个树也会受到影响。因此，我们必须不断与父节点交换，直到达到根节点为止。

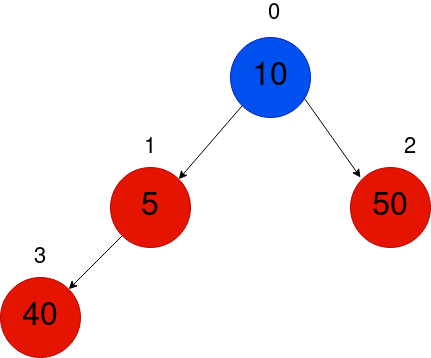
所以，我们还需要进行一次交换，因为在以节点0为根的子树中，最小堆的属性再次被违反了。

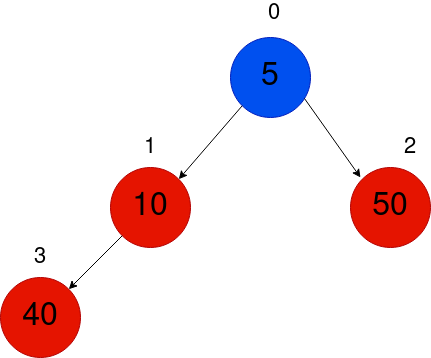
好的，既然我们已经可视化了，那就把它写下来吧！

MinHeap* insert_minheap(MinHeap* heap, int element) {
    // Inserts an element to the min heap
    // We first add it to the bottom (last level)
    // of the tree, and keep swapping with it's parent
    // if it is lesser than it. We keep doing that until
    // we reach the root node. So, we will have inserted the
    // element in it's proper position to preserve the min heap property
    if (heap->size == heap->capacity) {
        fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
        return heap;
    }
    // We can add it. Increase the size and add it to the end
    heap->size++;
    heap->arr[heap->size - 1] = element;

    // Keep swapping until we reach the root
    int curr = heap->size - 1;
    // As long as you aren't in the root node, and while the 
    // parent of the last element is greater than it
    while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
        // Swap
        int temp = heap->arr[parent(curr)];
        heap->arr[parent(curr)] = heap->arr[curr];
        heap->arr[curr] = temp;
        // Update the current index of element
        curr = parent(curr);
    }
    return heap; 
}

我们现在要实施删除方法。 .)

从最小堆中删除

在我们查看删除任何索引位置的元素之前，由于最小堆与根节点密切相关，我们将首先查看删除根节点的情况。

要删除最小元素（即根元素），我们将执行以下操作：

• Update the root as the last element of the array (tree)
• We will now remove the last element at the bottom. This is similar to swapping and deleting at the end! Only because we don’t care about the root value anymore, we simply update it instead.
• The problem again is that we need to maintain the min-heap property.
• So we must ensure that the whole tree maintains this property. We will use a function called heapify() to do this for us.

所以，我们知道在执行heapify()方法之后，删除方法将完成。

MinHeap* delete_minimum(MinHeap* heap) {
    // Deletes the minimum element, at the root
    if (!heap || heap->size == 0)
        return heap;

    int size = heap->size;
    int last_element = heap->arr[size-1];
    
    // Update root value with the last element
    heap->arr[0] = last_element;

    // Now remove the last element, by decreasing the size
    heap->size--;
    size--;

    // We need to call heapify(), to maintain the min-heap
    // property
    heap = heapify(heap, 0);
    return heap;
}

堆化（heapify()）的过程

这个函数接受一个元素的索引index，并通过与其直接子树中最小的元素交换来保持最小堆的性质。

生成的树将满足最小堆性质。

这涉及找到子树中的最小元素，并与当前元素进行交换。

在这之后，我们还需要确保整个树满足这一条件。所以，我们需要递归地在最小元素上调用这个过程，直到达到根节点为止！

MinHeap* heapify(MinHeap* heap, int index) {
    // Rearranges the heap as to maintain
    // the min-heap property
    if (heap->size <= 1)
        return heap;
    
    int left = left_child(index); 
    int right = right_child(index); 

    // Variable to get the smallest element of the subtree
    // of an element an index
    int smallest = index; 
    
    // If the left child is smaller than this element, it is
    // the smallest
    if (left < heap->size && heap->arr[left] < heap->arr[index]) 
        smallest = left; 
    
    // Similarly for the right, but we are updating the smallest element
    // so that it will definitely give the least element of the subtree
    if (right < heap->size && heap->arr[right] < heap->arr[smallest]) 
        smallest = right; 

    // Now if the current element is not the smallest,
    // swap with the current element. The min heap property
    // is now satisfied for this subtree. We now need to
    // recursively keep doing this until we reach the root node,
    // the point at which there will be no change!
    if (smallest != index) 
    { 
        int temp = heap->arr[index];
        heap->arr[index] = heap->arr[smallest];
        heap->arr[smallest] = temp;
        heap = heapify(heap, smallest); 
    }

    return heap;
}

我们现在可以扩展这个delete_minimum()函数，来删除任何元素。

删除一个任意元素

这仅涉及将所需元素设置为最小可能值，即get_min()-1，因为它必须小于当前最小值。

我们现在将继续交换，直到更新位置，使新的根节点成为该元素。

现在，我们回到了我们旧的delete_minimum()函数！我们可以简单地删除新的根节点！

有了这个，我们整个删除过程将如下所示：

MinHeap* delete_element(MinHeap* heap, int index) {
    // Deletes an element, indexed by index
    // Ensure that it's lesser than the current root
    heap->arr[index] = get_min(heap) - 1;
    
    // Now keep swapping, until we update the tree
    int curr = index;
    while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
        int temp = heap->arr[parent(curr)];
        heap->arr[parent(curr)] = heap->arr[curr];
        heap->arr[curr] = temp;
        curr = parent(curr);
    }

    // Now simply delete the minimum element
    heap = delete_minimum(heap);
    return heap;
}

唉！我们终于完成了。我现在会展示给你整个代码，包括print()函数，来可视化这棵树。

---

完整的代码（ de ）

#include <stdio.h>
#include <stdlib.h>

typedef struct MinHeap MinHeap;
struct MinHeap {
    int* arr;
    // Current Size of the Heap
    int size;
    // Maximum capacity of the heap
    int capacity;
};

int parent(int i) {
    // Get the index of the parent
    return (i - 1) / 2;
}

int left_child(int i) {
    return (2*i + 1);
}

int right_child(int i) {
    return (2*i + 2);
}

int get_min(MinHeap* heap) {
    // Return the root node element,
    // since that's the minimum
    return heap->arr[0];
}

MinHeap* init_minheap(int capacity) {
    MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
    minheap->arr = (int*) calloc (capacity, sizeof(int));
    minheap->capacity = capacity;
    minheap->size = 0;
    return minheap;
}

MinHeap* insert_minheap(MinHeap* heap, int element) {
    // Inserts an element to the min heap
    // We first add it to the bottom (last level)
    // of the tree, and keep swapping with it's parent
    // if it is lesser than it. We keep doing that until
    // we reach the root node. So, we will have inserted the
    // element in it's proper position to preserve the min heap property
    if (heap->size == heap->capacity) {
        fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
        return heap;
    }
    // We can add it. Increase the size and add it to the end
    heap->size++;
    heap->arr[heap->size - 1] = element;

    // Keep swapping until we reach the root
    int curr = heap->size - 1;
    // As long as you aren't in the root node, and while the 
    // parent of the last element is greater than it
    while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
        // Swap
        int temp = heap->arr[parent(curr)];
        heap->arr[parent(curr)] = heap->arr[curr];
        heap->arr[curr] = temp;
        // Update the current index of element
        curr = parent(curr);
    }
    return heap; 
}

MinHeap* heapify(MinHeap* heap, int index) {
    // Rearranges the heap as to maintain
    // the min-heap property
    if (heap->size <= 1)
        return heap;
    
    int left = left_child(index); 
    int right = right_child(index); 

    // Variable to get the smallest element of the subtree
    // of an element an index
    int smallest = index; 
    
    // If the left child is smaller than this element, it is
    // the smallest
    if (left < heap->size && heap->arr[left] < heap->arr[index]) 
        smallest = left; 
    
    // Similarly for the right, but we are updating the smallest element
    // so that it will definitely give the least element of the subtree
    if (right < heap->size && heap->arr[right] < heap->arr[smallest]) 
        smallest = right; 

    // Now if the current element is not the smallest,
    // swap with the current element. The min heap property
    // is now satisfied for this subtree. We now need to
    // recursively keep doing this until we reach the root node,
    // the point at which there will be no change!
    if (smallest != index) 
    { 
        int temp = heap->arr[index];
        heap->arr[index] = heap->arr[smallest];
        heap->arr[smallest] = temp;
        heap = heapify(heap, smallest); 
    }

    return heap;
}

MinHeap* delete_minimum(MinHeap* heap) {
    // Deletes the minimum element, at the root
    if (!heap || heap->size == 0)
        return heap;

    int size = heap->size;
    int last_element = heap->arr[size-1];
    
    // Update root value with the last element
    heap->arr[0] = last_element;

    // Now remove the last element, by decreasing the size
    heap->size--;
    size--;

    // We need to call heapify(), to maintain the min-heap
    // property
    heap = heapify(heap, 0);
    return heap;
}

MinHeap* delete_element(MinHeap* heap, int index) {
    // Deletes an element, indexed by index
    // Ensure that it's lesser than the current root
    heap->arr[index] = get_min(heap) - 1;
    
    // Now keep swapping, until we update the tree
    int curr = index;
    while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
        int temp = heap->arr[parent(curr)];
        heap->arr[parent(curr)] = heap->arr[curr];
        heap->arr[curr] = temp;
        curr = parent(curr);
    }

    // Now simply delete the minimum element
    heap = delete_minimum(heap);
    return heap;
}

void print_heap(MinHeap* heap) {
    // Simply print the array. This is an
    // inorder traversal of the tree
    printf("Min Heap:\n");
    for (int i=0; i<heap->size; i++) {
        printf("%d -> ", heap->arr[i]);
    }
    printf("\n");
}

void free_minheap(MinHeap* heap) {
    if (!heap)
        return;
    free(heap->arr);
    free(heap);
}

int main() {
    // Capacity of 10 elements
    MinHeap* heap = init_minheap(10);

    insert_minheap(heap, 40);
    insert_minheap(heap, 50);
    insert_minheap(heap, 5);
    print_heap(heap);
    
    // Delete the heap->arr[1] (50)
    delete_element(heap, 1);

    print_heap(heap);
    free_minheap(heap);
    return 0;
}

输出

Min Heap:
5 -> 50 -> 40 -> 
Min Heap:
5 -> 40 -> 

---

实现的时间复杂度

上述过程的时间复杂度如下所示：

---

下载这个代码。

你可以从我上传的Github Gist中下载完整的代码。如果对此有任何疑问，请在下面的评论区询问！

---

结论 (jié

在这篇文章中，我们学习了如何表示最小堆二叉树，并且还看了一种在C语言中的实现方式。

参考文献

• An illustration of Heaps, from Cormen
• Wikipedia article on Binary Heaps

---